论文导读::本文首先对伊藤过程的理论推导进行概述。在理论回顾的基础上,讨论了股票价格变化的伊藤过程,并在假设不分红利的情况下,进行股票价格动态的模拟实验。然后,又对伊藤过程的预测效果进行了实证研究。
论文关键词:布朗运动,伊藤过程,股票价格
价格是金融工程的核心问题,金融产品价格的确定和预测一直是理论界和实务界的热点问题,尤其对于股票价格的变化规律,人们使用各种方法和工具进行了很多的研究。本文采用实证方法,利用描述股票价格变化的伊藤过程,对此进行了研究。
一、理论概述
(一)倍数模型
倍数模型认为任何时间的资产价格都在某种程度上依赖于以前的价格,模型具有如下形式:

其中 表示时间k的资产价格。变量 表示时间k的资产价格。变量 规定了时间k与时间k+1之间的价格相对变化,这个相对变化是 规定了时间k与时间k+1之间的价格相对变化,这个相对变化是 ,它既独立于 ,它既独立于 ,也独立于价格单位,且每个 ,也独立于价格单位,且每个 (k=0,1,2,…,N-1)是相互独立的随机变量。 (k=0,1,2,…,N-1)是相互独立的随机变量。
在方程两边取自然对数,倍数模型将变为:

(二)随机游走和维纳过程
为了得到股票价格的连续时间模型布朗运动,需要在倍数模型中引入特殊的时间的随机函数,称为随机游走和维纳过程。
假定有N个长度为 的时期,通过如下关系式定义可加过程z: 的时期,通过如下关系式定义可加过程z:


其中 。这个过程被称为随机游走。在这个方程中, 。这个过程被称为随机游走。在这个方程中, 是均值为0,方差为1的随机变量――标准化正态随机变量,这些随机变量是互不相关的。这个随机游走过程开始于 是均值为0,方差为1的随机变量――标准化正态随机变量,这些随机变量是互不相关的。这个随机游走过程开始于 ,之后根据随机变量 ,之后根据随机变量 的随机性变化形成一个特定的轨道。 的随机性变化形成一个特定的轨道。
控制论的发明人维纳在1923年指出,布朗运动在数学上是一个随机过程,提出了用“随机微分方程”来描述,因此人们也把布朗运动称为维纳过程。当 时,将随机游走过程取极限就得到一个维纳过程,将表示维纳过程的方程符号化后写成: 时,将随机游走过程取极限就得到一个维纳过程,将表示维纳过程的方程符号化后写成:

其中 是标准正态随机变量。当 是标准正态随机变量。当 时,随机变量 时,随机变量 与 与 是不相关的。对维纳过程的这种描述并不严格,但它提供了一个很好的直觉描述。 是不相关的。对维纳过程的这种描述并不严格,但它提供了一个很好的直觉描述。
维纳过程(或布朗运动)是所有其他更一般的过程的基本构建材料,这种一般化是通过在场微分方程中加入白噪声而实现的论文格式范文。一般化程序中最简单的拓展就是广义维纳过程,它具有如下形式:
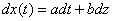
这里对于t, 是随机变量,z是维纳过程,a和b是常数。 是随机变量,z是维纳过程,a和b是常数。
(三)伊藤过程
日本数学家伊藤发展建立了带有布朗运动干扰项的随机微分方程,该方程描写的过程就是伊藤过程,具有如下形式:

其中z表示维纳过程。但是,现在的系数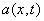 和 和 可能取决于x和t。伊藤过程可看成为一般化的维纳过程,它直接把布朗运动理解为随机干扰,从而赋予了布朗运动最一般的意义。 可能取决于x和t。伊藤过程可看成为一般化的维纳过程,它直接把布朗运动理解为随机干扰,从而赋予了布朗运动最一般的意义。
(四)股票价格变化的伊藤形式
布朗运动是随机涨落的典型现象,一般地说,许许多多的宏观观测都要受到布朗运动的限制。法国经济学家Bachelier把股价的变动理想化为布朗运动,在此基础上,经济学家把伊藤过程方程用于描写股票价格的行为过程,伊藤过程已成为采用最为广泛的描述股票价格变化的随机过程模型。
首先将前面提高的股票价格的倍数模型扩展为连续时间模型,形式为:

这里v和 是常数,而z是标准维纳过程。方程的整个右边是随机变量 是常数,而z是标准维纳过程。方程的整个右边是随机变量 在离散事件模型中所扮演的角色,它可以看成是一个常数加上一个零均值的正态随机变量,因此布朗运动,从总体上看,它是一个正态随机变量。 在离散事件模型中所扮演的角色,它可以看成是一个常数加上一个零均值的正态随机变量,因此布朗运动,从总体上看,它是一个正态随机变量。
应用 方便了模型的推导,并且体现了该随机过程是对数正态分布倍数模型的直接推广。但是,用 方便了模型的推导,并且体现了该随机过程是对数正态分布倍数模型的直接推广。但是,用 本身来表示这个随机过程是很有用的。 本身来表示这个随机过程是很有用的。
在普通微积分中,我们知道:

但在伊藤过程中改变变量时必须应用一个矫正项。用 表示的适当的伊藤过程是: 表示的适当的伊藤过程是:

注意到矫正项恰好与对数正态随机变量的期望值表达式要求的一样。令 ,于是可以将这个方程写成价格动态的标准伊藤过程: ,于是可以将这个方程写成价格动态的标准伊藤过程:

其中 可以认为是股票的回报微分。 可以认为是股票的回报微分。
因此,为更确切地描写股票价格的行为过程,伊藤过程方程被修正为:

其中S表示股票价格, 为股票价格的预期收益率, 为股票价格的预期收益率, 为股票价格波动率,z是标准维纳过程。等式右边表示 为股票价格波动率,z是标准维纳过程。等式右边表示 时间内股票的收益,其中第一项 时间内股票的收益,其中第一项 表示这种收益的期望值,第二项 表示这种收益的期望值,第二项 表示这种影响期望收益的随机因素。 表示这种影响期望收益的随机因素。
人们把这个方程称为股价方程,由伊藤过程描述的股价方程是一个正向的随机微分方程。从确定的 出发,根据布朗运动的随机变量在0-t之间的形态来推断轨线的统计行为。 出发,根据布朗运动的随机变量在0-t之间的形态来推断轨线的统计行为。
由伊藤方程可以推导出,股票价格的变化服从对数正态分布,即:

而且有:
 , ,
由正态分布的性质可知:

很明显,若假设 由 由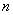 个细分的时间段 个细分的时间段 组成,即 组成,即 ,且由马尔可夫性每个 ,且由马尔可夫性每个 时段内价格的变化相对独立,则由正态分布方差的可加性,标准差 时段内价格的变化相对独立,则由正态分布方差的可加性,标准差 可以看作 可以看作 时段内价格变化的标准差加和而成。 时段内价格变化的标准差加和而成。
1/2 1 2 下一页 尾页 |


