论文导读::首次引入多元正态混合GARCH模型(MNM-GARCH),并运用于沪深股市波动性特征和动态相关结构的实证研究当中,研究结果发现相比传统的MV GARCH模型,MNM-GARCH模型对沪深股市波动特征及二者之间关联性的解释效果更优,充分体现了该模型的优越性。同时利用广义似然比检验法,构造广义似然比统计量检验上述结论,检验结果支持上述结论。
论文关键词:MNM-GARCH模型,波动性,动态相关性,广义似然比检验
一、引言
Engle(1982)开创性地提出了ARCH模型,Bollerslev(1986)并将其扩展至GARCH模型,
自此之后对单一金融资产波动性的建模研究得到了快速发展,形成了一套成熟而又完备的理论框架。然而在金融市场中,不同的市场、资产之间,往往存在着相互影响和波动的相互关系以及风险的相互传递。为分散、化解金融风险,就需要对多个资产进行组合,进行风险的对冲和规避,这些都是建立在对多个变量、多个市场之间波动相关特性的分析基础之上 。因此,多元GARCH模型开始迅速发展,成为多年来计量经济学研究的重要内容。文献[2]对多种MV GARCH模型做了相关综述,总结了这些模型的基本框架、适用条件及模型优劣。 。因此,多元GARCH模型开始迅速发展,成为多年来计量经济学研究的重要内容。文献[2]对多种MV GARCH模型做了相关综述,总结了这些模型的基本框架、适用条件及模型优劣。
近年来,由于在风险管理方面的重要应用,关于金融波动的动态混合模型越来越受到关注,而这种动态混合模型是基于多元正态混合分布假设的。实证研究表明,若干个正态分布的有限混合能够有效捕捉到收益率分布中的有偏和厚尾,而且当其与GARCH类方程结合来刻画各混合成分的方差时,还能产生较复杂的动态行为,而这种行为现象在股市中经常出现。例如,混合结构中的一个成分是平稳的,而另一个成分不平稳,但它们的混合过程仍然表现为平稳的。这就相当于股市大部分时间是稳定的,偶尔出现短期的剧烈波动 。 。
目前,国外学者已对单变量的正态混合GARCH(NM-GARCH)模型进行了大量研究金融论文,包括Haas et al.(2004),Alexanderand Lazar(2006),Bauwens and Rombouts(2007),Bertholonet al.(2006),Wu and Lee(2007),Ausin and Galeano(2007),Giannikiset al.(2008)等等。他们对多项金融资产的研究结论均表明,正态混合GARCH模型对金融资产的波动率能够进行很好地建模和预测,并且无论在样本内或样本外的表现都优于其他一些GARCH模型。由于实际应用中我们大多研究的是多元资产,例如在投资组合管理中,我们最关心的是多种资产之间的相关性,因为相关性的大小决定了我们能够通过分散化组合投资减少多大风险 。Haas et al.(2006)(2009),Bauwenset al.(2007)把一元NM-GARCH模型推广到多元情形,得到了多元正态混合GARCH模型(MNM-GARCH),并将其应用到道琼斯指数和纳斯达克指数日收益率的研究上,结果发现在高维情形时,具有很少参数的简单模型的混合相比复杂的单一模型具有更强的适应性和灵活性 。Haas et al.(2006)(2009),Bauwenset al.(2007)把一元NM-GARCH模型推广到多元情形,得到了多元正态混合GARCH模型(MNM-GARCH),并将其应用到道琼斯指数和纳斯达克指数日收益率的研究上,结果发现在高维情形时,具有很少参数的简单模型的混合相比复杂的单一模型具有更强的适应性和灵活性 。国内很少有学者做过此方面 。国内很少有学者做过此方面
研究,张明恒、程乾生(2002)对外汇银行同业拆借市场和中国股票市场的金融资产收益分布分别进行了混合高斯分析,结果发现这些金融资产的收益分布不是一个纯粹的高斯分布,但可以由有限个高斯分布混合组成 ;徐光林(2006)利用混合高斯分布研究了上证指数的波动性,结果表明正态混合分布假设下的GARCH模型可以较好的解释上证指数的波动性 ;徐光林(2006)利用混合高斯分布研究了上证指数的波动性,结果表明正态混合分布假设下的GARCH模型可以较好的解释上证指数的波动性 。但是,这些研究仅仅局限于单个市场或金融资产,对多种资产或市场之间的波动性以及动态相关结构缺乏研究和深入分析。 。但是,这些研究仅仅局限于单个市场或金融资产,对多种资产或市场之间的波动性以及动态相关结构缺乏研究和深入分析。
鉴于此,笔者首次引入和运用MNM-GARCH模型,对沪深股市收益的波动性及相互关系进行了研究,并进一步分析了二者之间的动态相关性,同时提出了用广义似然比检验法来检验此模型描述沪深股市动态相关结构的充分性,为投资组合管理和风险管理提供了一种新的研究方法。
二、理论模型与研究方法概述
MNM-GARCH模型不同于以往的MVGARCH模型基于多元正态分布的假设,它建立在多元正态混合分布的假设基础上,即收益分布是由若干个多元正态分布混合组成,而每个分布的方差-协方差阵满足MV GARCH模型,文献[3]、[4]、[7]给出了此模型的具体形式。
(一)MNM(k)-GARCH(1,1)模型
设 是一个二元收益率时间序列向量,给定均值方程如下: 是一个二元收益率时间序列向量,给定均值方程如下:
 (1) (1)
其中, 和 和 为随机误差项。 为随机误差项。
文献[3][4][7]指出,一个二维随机误差向量 服从k-成分多元正态混合分布, 服从k-成分多元正态混合分布, ,如果其密度函数满足: ,如果其密度函数满足:
 ,(2) ,(2)
其中: 为t-1时刻的信息集论文开题报告。 为t-1时刻的信息集论文开题报告。 ,称为混合权重,表示波动来自第j个成分的概率, ,称为混合权重,表示波动来自第j个成分的概率, 。第j个成分的概率密度为 。第j个成分的概率密度为
 (3) (3)
通常限定 ,则 ,则 的条件一阶、二阶矩为 的条件一阶、二阶矩为
 (4) (4)
记 ,则各成分的协方差矩阵满足 ,则各成分的协方差矩阵满足
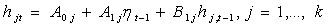 (5) (5)
其中 是3×1阶列向量, 是3×1阶列向量, 、 、 是3×3阶方阵, 是3×3阶方阵, 。 。
为保证所有条件协方差矩阵的正定性, ( ( )由BEKK(1,1)模型给出(以下简记为MNM-BEKK),具体如下: )由BEKK(1,1)模型给出(以下简记为MNM-BEKK),具体如下:
 (6) (6)
其中 是下三角矩阵。 是下三角矩阵。
估计出(6)中的 后,(5)中 后,(5)中 和 和 可以通过下式得到 可以通过下式得到
 
1/3 1 2 3 下一页 尾页 |


