论文导读:：实证研究人民币汇率变动对安徽省贸易进出口的影响。人民币汇率波动与风险价值研究。
论文关键词：人民币汇率，风险价值，GARCH，半参数法
一、 引言
人民币汇率一直是国际国内高度关注的问题，外界普遍要求人民币升值，对人民币升值的速度也一直是热议的话题。我国从2005年7月21日实行汇改后，人民币持续不断升值，人民币汇率风险逐渐显现，而且汇率的持续波动加大了人民币的汇率风险。2009年以来我国经济率先走出金融危机的阴影，呈现出快速复苏的势头，国际上要求人民币升值的呼声再次高涨。人民币升值对于我们来说既有利又有弊，但人民币升值过快将增加汇率风险，而且会对我国的宏观经济带来很大冲击。因此，研究人民币汇率的波动，以及正确测量汇率风险，就显得十分必要。
本文选取人民币/美元汇率中间价的日数据作为研究对象，利用GARCH模型分析了人民币汇率的波动特性；同时，采用基于GARCH模型的VaR估计方法（参数法）和David X Li（1999）提出的半参数估计法实证检验，分别度量了人民币汇率的风险价值，并对两种方法进行了比较。
二、 理论模型与研究方法
1.GARCH模型
自回归条件异方差(ARCH)模型最早是由Engle于1982年提出半参数法，用于波动性的建模研究。在此基础上，Bollersler进行了扩展，于1986年提出广义自回归条件异方差模型，即GARCH模型。
GARCH(p，q)模型定义如下：
均值方程： ，
波动率方程： 
其中，{ }是均值为0，方差为1 的独立同分布随机变量序列， ＞0, ≥0 ( )， ≥0 ( )。实际中，通常假定服从标准正态分布，学生-t分布，或广义误差分布（GED）。
2.单整GARCH（IGARCH）模型
在实际研究中，人们常发现GARCH模型的a参数和β参数的和非常接近于1，在这种情况下，条件方差具有单位根和单整性，于是人们将符合这种特征的GARCH模型称作单整GARCH模型小论文。
当GARCH模型的估计参数满足：
时，就称作单整GARCH模型，记为IGARCH模型。该模型描述了条件方差波动的持续性质。
3.VaR方法
（1）基于GARCH模型的VaR度量
VaR即风险价值，是指在正常的市场条件和给定的置信水平下，某一金融资产在未来特定一段持有期内的最大损失。用统计学公式表示即为：
其中， c 为置信水平。
通常为简化计算，会假设资产收益服从正态分布，则VaR可表示为
 （1）
其中， 是置信度为a的标准正态分布的临界值，当a=5%时， ； 是收益率序列的条件方差。
（2）基于David X.Li半参数估计方法的VaR度量
上述计算VaR的过程中需假设收益服从正态分布，然而现实中的许多收益序列分布都具有“厚尾”现象，所以利用正态分布假设常常会低估潜在的风险。David Li（1999）提出了基于收益率序列的均值、标准差、偏度和峰度的半参数法，该方法不需做任何分布假设，即可构造VaR。假设收益率序列r的均值、标准差、偏度和峰度分别为：
若 ≠0， ≠0，则r不服从正态分布。可以证明，VaR的置信上限VaR(U)和置信下限VaR(L)可以用下面的公式计算得到：
 （2）
 （3）
其中半参数法，≠0； 是标准正态分布的临界值。
（3）VaR模型的事后检验
VaR是一个统计估计值，其准确程度受到估计误差的影响，故需进行严格的检验。通行的检验法则是通过“失败率”来检验，将各期的收益率r与VaR进行对比，当收益率超过VaR时记为失败，此时记1，否则记0。若考察实际天数为T，失败天数为N，则失败率p=N/T，然后将p与显著性水平a进行比较，来判定模型的准确性。若p>a，说明模型低估了风险；若p<a，表明模型的预测结果覆盖了实际的损失，但如果p太小，则表明模型估计过于保守。
三、 实证分析
1.数据选取及处理
本文选取2009年1月5日—2010年6月2日为样本期，以人民币/美元汇率中间价为研究对象，对其短期波动特性进行描述。数据来源于国家外汇管理局网站（http://www.safe.gov.cn），变量名称记为P。分析时作如下处理： ，作为汇率的收益率。对数据的操作与处理及模型的估计与检验是在计量经济学软件Eviews6.0上实现的。
2.GARCH模型的估计及检验
表1给出了收益率序列的基本统计特征值，从中可以看出，收益率基本上在零上下波动，峰度显著大于3，呈现出明显的尖峰和厚尾的特征，同时根据JB统计量可知，其不服从正态分布，因此不能简单地用正态分布模拟人民币汇率收益率的变化。根据对相关图的判别，我们可初步得出收益率序列符合平稳性的特征，表2给出了对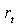 进行单位根检验的结果，在各种水平下都接受了序列平稳性的假设，表明收益率序列是平稳的。另外，由 的ACF和PACF函数图像可知，可以用ARMA（2,2）模型对其进行拟合，然后对残差序列进行ARCH-LM检验，检验结果见表3半参数法，结果表明，在95%的置信水平下，拒绝原假设，收益率序列存在AHCH效应。也可用残差平方相关图检验，残差平方自相关（AC）和偏相关（PAC）系数显著不为零，且Ｑ统计量也非常显著，可得到同样的检验结果。因此需要采用GARCH模型来准确描述收益率序列 的波动性特征小论文。
表1 人民币汇率收益率序列的统计特征
|
样本容量
|
均值
|
最大值
|
最小值
|
标准差
|
偏度
|
峰度
|
JB-统计量
|
|
343
|
-2.76E-06
|
0.000732
|
-0.000731
|
0.000163
|
0.72902
|
6.2865
|
155.5714
|
表2 人民币汇率收益率序列的ADF检验
|
ADF-统计量
|
-15.79359
|
1% level
|
-3.449220
|
|
5% level
|
-2.869750
|
|
10% level
|
-2.571213
|
表3 ARMA（2,2）模型残差序列ARCH-LM检验结果
|
F-statistic
|
3.288543
|
Prob. F(2,337)
|
0.0385
|
|
Obs*R-squared
|
6.330941
|
Prob. Chi-Square(2)
|
0.0422
|
在以上模型及检验分析的基础上，经过变量筛选、模型参数和各种统计显著性检验、以及AIC和SC值的比较分析，最终确定采用ARMA(2,2)-IGARCH(1,1)-t模型，模型的估计结果如表4。
1/2 1 2 下一页 尾页 |
