论文导读::动态投资组合风险的控制模型[1]。风险控制一直是各大金融机构研究的中心问题。基于多维GARCH提出的[7~8]。
论文关键词:动态投资组合,风险控制,GARCH
1 引言
风险控制一直是各大金融机构研究的中心问题,国内外大量文献的研究大都停留在对投资组合静态风险的研究上,如,Markowitz (1952) 最早定量研究了投资组合问题, 并把投资组合的方差作为风险度量指标[1] ,Ouderri 等(1991) 和Green 等(1992) 把半方差作为风险度量指标[2~3] ,Konno等(1994,1998) 把绝对离差作为风险度量指标[4~5],Philippe (1996) 最早把VaR作为风险度量指标, 而这些度量指标均是静态的[6]。事实上,单项资产的收益率的波动性并不是固定的,而是有规律的,即当期的波动对以后各期的波动都具有长期的影响,表现为收益率波动的持续性,这就启发我们需要从动态的角度来审视和控制风险,使得我们选择的投资组合的当期收益率波动对以后各期的收益率波动的影响减弱,实际上也就是减弱投资组合后期的风险,从而使得金融机构在进行投资时把风险控制到最小GARCH,即使的投资组合收益率表现出较弱的持续性。方差持续性及协同持续定义是由Bollerslev和Engle (1988,1993)基于多维GARCH提出的[7~8]。 本文基于协同持续思想,运用GARCH 模型和二次规划技术建立了动态投资组合风险控制模型, 并得到了相应的投资组合权重,这将对投资组合风险控制问题具有理论和实践意义。
2 动态投资组合风险的控制模型 [1]
2.1多维GARCH模型及协同性定义
Bollerslev和Engle(1988,1993)提出了多维GARCH模型:
 (1) (1)
其中, 表示 表示 维资产收益率 维资产收益率 的均值, 的均值, 表示一个 表示一个 维的随机扰动项,并且 维的随机扰动项,并且 , , 是直到 是直到 时的信息集, 时的信息集, 是资产组合的方差-协方差矩阵,并且是关于 是资产组合的方差-协方差矩阵,并且是关于 可测的 可测的 维的正定矩阵, 维的正定矩阵, 为 为 维向量, 维向量, 和 和 均是 均是 维方阵,且 维方阵,且 和 和 使得 使得 正定, 正定, 。 。
Bollerslev和Engle(1988,1993)在多维GARCH模型的基础上提出了金融资产收益率方差协同性持续和方差持续性定义。
方差持续性定义:
在描述多项资产收益率方差变化的多维GARCH模型中:
令 ,对于一些 ,对于一些 ,如果 ,如果 ,则认为多项资产的收益率序列 ,则认为多项资产的收益率序列 具有非常持续性。 具有非常持续性。
其中,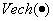 表示向量半算子或者是拉直向量,按列堆积方阵的下三角矩阵, 表示向量半算子或者是拉直向量,按列堆积方阵的下三角矩阵, 表示基于信息集 表示基于信息集 对向量 对向量 的条件期望,然而, 的条件期望,然而, 表示对向量 表示对向量 的期望, 的期望, 表示向量 表示向量 的第 的第 个分量, 个分量,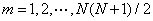 。 。
方差协同持续性定义:
如果多项资产收益率序列 是方差持续的,并且在 是方差持续的,并且在 条件下,有 条件下,有 ,那么多项资产收益率序列 ,那么多项资产收益率序列 是方差持续的论文格式。 是方差持续的论文格式。
其中: 为 为 维的列向量。 维的列向量。
从投资组合的角度解释为:单项资产的历史收益会影响其未来的收益,并且并不会随着时间的推移而消失,而通过对资产权重的适当分配GARCH,使资产组合的历史信息对其未来收益率不表现出长期的影响,以此来减少投资组合收益的不确定性。
2.2金融资产收益率方差
Engle在1982年提出ARCH模型,1988年Bollerslev把ARCH模型扩展为GARCH(p,q)模型,该模型能准确的刻画金融资产波动的时变形和聚集性。
用GARCH(p,q)模型描述金融资产收益率方差序列为:
 (2) (2)
其中, 代表金融资产的编号, 代表金融资产的编号,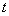 为投资期, 为投资期, 代表 代表 金融资产在 金融资产在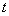 时期的收益率, 时期的收益率, 代表 代表 金融资产在 金融资产在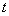 时期的均值, 时期的均值, , , 是 是 金融资产在 金融资产在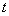 时期的的方差。 时期的的方差。
1/3 1 2 3 下一页 尾页 |


