本文所采用的退税率按相应产品的征税率来计算。第二,计算退税额时的“税基”[3]问题。直接用出口货物的离岸价格作为出口退税的“税基”是不合适的,用出口货物的产成品成本并用“倒算法”更科学。幸而投入产出表在设计时,出口商品采用国内生产者价格而不是采用离岸价格。因此,在测算出口退税额时,“税基”直接用投入产出表中的国内生产者价格。第三,增值税所涉及到中央与地方的财政体制问题。增值税的征收与退还是一个“对称”问题。增值税在征收时,中央与地方是“三一分成”(即中央得75%,地方得25%);那么,增值税在出口退税时,也应该中央与地方“三一分担”(即中央分担75%,地方分担25%)。综合考虑这三个问题,全部应由贵州省承担的增值税出口退税额(令其为 )用数学表达为: )用数学表达为:
 (2.11) (2.11)
 (2.12) (2.12)
其中, 代表由各种产品的征税率为元素的行向量。 代表由各种产品的征税率为元素的行向量。
(2.11)式的经济学意义很明显,即:贵州省的“直接出口”部分、贵州省通过流到贵州省外的中国大陆省份所“间接出口”或“引致出口”部分、贵州省产出的增加值部分所带来的出口部分,这三者所含的增值税乘以财政体制的25%。
证明:
 表示源于贵州省的“直接出口”部分中所包含的“付现增值税”, 表示源于贵州省的“直接出口”部分中所包含的“付现增值税”, 表示源于贵州省通过流到贵州省外的中国大陆省份所“间接出口”或“引致出口”部分中所包含的“付现增值税”, 表示源于贵州省通过流到贵州省外的中国大陆省份所“间接出口”或“引致出口”部分中所包含的“付现增值税”, 表示贵州省产出的增加值部分所带来的出口部分中所包含的“付现增值税”。 表示贵州省产出的增加值部分所带来的出口部分中所包含的“付现增值税”。 可以分解成两个部分相乘, 可以分解成两个部分相乘, 贵州省的出口货物价值量的列向量, 贵州省的出口货物价值量的列向量, 既可以理解为“广义的”出口退税率行向量,又可理解为考虑了出口退税率后的直接物耗系数行向量,二者( 既可以理解为“广义的”出口退税率行向量,又可理解为考虑了出口退税率后的直接物耗系数行向量,二者( 与 与 )相乘可以理解为税率乘以“税基”。对 )相乘可以理解为税率乘以“税基”。对 也可做同样的分解和分析。 也可做同样的分解和分析。
证毕。
贵州省应承担的份额被计算出来后,余下来的则由中央政府承担。
值得注意的是,投入产出表中列示的有应征收营业税的其他服务业,在计算(2.11)式的 过程中是否要剔除出来?其实, 过程中是否要剔除出来?其实, 是一个以各种产品的征税率为元素的行向量,其中应征营业税的服务业(其增值税的税率可看成为0)的“征税率”和“退税率”均为0,因此通过矩阵的乘法运算自然而然地会被“剔除”掉。这也是投入产出模型和矩阵运算在处理本文问题的魅力所在。 是一个以各种产品的征税率为元素的行向量,其中应征营业税的服务业(其增值税的税率可看成为0)的“征税率”和“退税率”均为0,因此通过矩阵的乘法运算自然而然地会被“剔除”掉。这也是投入产出模型和矩阵运算在处理本文问题的魅力所在。
4.算法步骤
综上所述,可以设计一个算法,具体步骤如下:
Step1取某年度(例如2002年)的“全国投入产出表”和同年度的“贵州省投入产出表”。
Step2检查“全国投入产出表”和“贵州省投入产出表”是否同型,用同型的“全国投入产出表”减“贵州省投入产出表”,得到“中国大陆除贵州之外的其他省份地区的投入产出表”,并得出 、 、 、 、 。 。
Step3把“贵州省投入产出表”的第一象限进行拆分,用以构造包含中国大陆除贵州之外的其他省份流入和境外流入的矩阵“中间投入×中间使用”,得出 和 和 。 。
Step4仿照Step3,把“中国大陆除贵州之外的其他省份投入产出表”的第一象限进行拆分,构造包含贵州省流入和境外流入的矩阵“中间投入×中间使用”,得出 。 。
Step5按定理3计算出S。
三、算例
1.数据来源说明及直接消耗系数矩阵处理
(1)《贵州省投入产出表(2002)》。根据上文分析,《贵州省投入产出表(2002)》是不能直接用于本文的研究的。原因有二:第一,源于《中国地区投入产出表2002》[4]的投入产出流量表为42个部门,且矩阵的宾栏“净流出”栏需要对“进口”、“出口”、“贵州流出省外”、“从外省流入贵州”进行处理。处理时,用《中国区域间投入产出表1997》[5]近似替代。本文把42个部门归并为8个部门,即分别为:“农业”、“采掘业”、“轻工业”、“重工业”、“电力及蒸汽、热水、煤气、自来水的生产和供应业”、“商业”、“建筑业”、“其他服务业”,相应地,这8个部门所对应的增值税征税率(或退税率)应分别为 。第二,因为《贵州投入产出表(2002)》是竞争型投入产出表,而本文需要将竞争型投入产出表改进为非竞争型投入产出表,因此需要借鉴部分专家(沈利生[6],2009;王玥、佟仁城、许健[7],2007)的“拆分法”。考虑中间产品流量的拆分。假设同一部门的国内产品和进口产品具有同质性,其他部门消耗该部门产品时,都按相同的比例拆分。在拆分第i部门的中间产品 。第二,因为《贵州投入产出表(2002)》是竞争型投入产出表,而本文需要将竞争型投入产出表改进为非竞争型投入产出表,因此需要借鉴部分专家(沈利生[6],2009;王玥、佟仁城、许健[7],2007)的“拆分法”。考虑中间产品流量的拆分。假设同一部门的国内产品和进口产品具有同质性,其他部门消耗该部门产品时,都按相同的比例拆分。在拆分第i部门的中间产品 时,令 时,令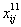 、 、 和 和 三者之间的比例等于该部门的国内总产出 三者之间的比例等于该部门的国内总产出 扣除流到国内其他省市的流出量再扣除贵州省出口量以后与国内其他省市流入量、进口量之比,即 扣除流到国内其他省市的流出量再扣除贵州省出口量以后与国内其他省市流入量、进口量之比,即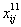 : : : : = = : : : : 。 。 3/4 首页 上一页 1 2 3 4 下一页 尾页 |


