因此,将表1再次修正为表2。表2跟表1比较,有如下变化:第一,从形式上看,表1的第Ⅰ象限是方阵,而表2的第Ⅰ象限不是方阵。第二,表1把贵州省的出口按照用途(中间使用和最终使用)进行分类,而表2却把贵州省的出口“简化”成外生变量 。“简化”成外生变量并不影响本文的研究,因此作此修正。 。“简化”成外生变量并不影响本文的研究,因此作此修正。
表2再次改进的价值型地区间投入产出表
|
产
投 出
入
|
中 间 使 用
|
最 终 使 用
|
总
产
出
|
|
贵州省
|
除贵州之外的中国大陆省市
|
|
其中:出口量
|
|
中
间
投
入
|
贵州省
|

|

|

|

|

|
|
除贵州之外的中国大陆省市
|

|

|

|

|

|
|
境外
|

|

|
|
|
|
|
最初投入合计
|

|

|
|
|
总投入
|

|

|
|
定理1(经营单位所在地为贵州的出口货物价值量的来源构成的地区分布定理)经营单位所在地为贵州的出口货物价值量可分解为四个部分:来源于贵州省的物耗量、来源于除了贵州省之外的中国大陆其他省市的物耗量、来源于境外的物耗量、来源于贵州省的最初投入量,该价值量为四个部分的代数和。
用数学符号表示为:
 (2.1) (2.1)
其中, 为“贵州省出口产品相对于贵州省总产出的分配系数对角阵”, 为“贵州省出口产品相对于贵州省总产出的分配系数对角阵”, 、 、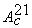 、 、 分别为贵州省对本地产品的直接物耗系数对角阵、贵州省对“除贵州之外的中国大陆省市”产品的直接物耗系数对角阵、贵州省对境外产品的直接物耗系数对角阵。 分别为贵州省对本地产品的直接物耗系数对角阵、贵州省对“除贵州之外的中国大陆省市”产品的直接物耗系数对角阵、贵州省对境外产品的直接物耗系数对角阵。
证明:
第一步,从列的方向计算贵州省各部门总产出列向量(通过行向量的转置即可)的投入结构,算出从“除贵州省之外的中国大陆省市”输入的产品列向量、进口的产品列向量,即
 (2.2) (2.2)
利用“∑”符号,上式可改写为:
 ( ( )(2.3) )(2.3)
引入直接消耗系数 、 、 、 、 后,将 后,将 , , , , ,代入上式,得 ,代入上式,得
 ( ( )(2.4) )(2.4)
设 ——直接消耗系数矩阵 ——直接消耗系数矩阵 中第 中第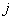 列元素之和,其含义是 列元素之和,其含义是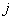 部门生产单位产值对所有物质产品的消耗量,称为贵州省对本地产品的直接物耗系数;同理, 部门生产单位产值对所有物质产品的消耗量,称为贵州省对本地产品的直接物耗系数;同理, 、 、 分别表示贵州省对“除贵州省之外的中国大陆省市”产品的直接物耗系数和贵州省对境外产品的直接物耗系数。 分别表示贵州省对“除贵州省之外的中国大陆省市”产品的直接物耗系数和贵州省对境外产品的直接物耗系数。
将上式改写成矩阵形式,则有
 (2.5) (2.5)
式中, , , , , 。 。
第二步,计算贵州省的出口向量占贵州省总产出向量的“比例”(即算出“贵州省出口产品分配系数对角阵” ),即 ),即
 (2.6) (2.6)
第三步,用贵州省总产出的投入结构表达贵州省的出口向量,即联系(2.5)式和(2.6)式,得
 (2.7) (2.7)
 (2.8) (2.8)
证毕。
2.定理2(在全国范围内的出口货物价值量应“归集”到贵州省政府的份额定理)在全国范围内的出口货物价值量应“归集”到贵州省政府的份额可分为三部分:贵州省的“直接出口”部分、贵州省通过流到贵州省外的中国大陆省份所“间接出口”或“引致出口”部分、贵州省产出的增加值部分所带来的出口,该份额为三个部分的代数和。
用数学符号表示为:
 (2.9) (2.9)
证明:
(2.8)式显示出了由贵州省出口的货物的来源于三个地区(即贵州、贵州之外的大陆各地、境外)的价值结构问题。其中,来源于贵州省的物耗量所形成的价值量 由贵州省承担,这是没有疑问的;来源于贵州省之外的大陆各地的价值量,尽管通过“价值链”的形成最终由贵州省口岸出口,但却不能由贵州省承担,即(2.8)式中的 由贵州省承担,这是没有疑问的;来源于贵州省之外的大陆各地的价值量,尽管通过“价值链”的形成最终由贵州省口岸出口,但却不能由贵州省承担,即(2.8)式中的 部分;来源于境外的价值量,其增值税由海关代征,入了中央金库,该部分价值量 部分;来源于境外的价值量,其增值税由海关代征,入了中央金库,该部分价值量 应全部由中央政府承担,不能由贵州省承担;来源于贵州省的最初投入量 应全部由中央政府承担,不能由贵州省承担;来源于贵州省的最初投入量 应由贵州省承担。同样,从贵州之外的大陆各地出口的货物中也有来源于贵州省的价值量问题,因此,尽管不是从贵州省口岸出口,也应由贵州省承担。这部分从贵州之外的大陆其他口岸出口的货物应由贵州省承担出口退税的价值量应等于 应由贵州省承担。同样,从贵州之外的大陆各地出口的货物中也有来源于贵州省的价值量问题,因此,尽管不是从贵州省口岸出口,也应由贵州省承担。这部分从贵州之外的大陆其他口岸出口的货物应由贵州省承担出口退税的价值量应等于 。因此,应由贵州省承担出口退税的价值量(令其为 。因此,应由贵州省承担出口退税的价值量(令其为 )为(2.9)。 )为(2.9)。
推论(在全国范围内的出口货物价值量应“归集”到贵州省政府的份额定理)在全国范围内的出口货物价值量应“归集”到贵州省政府的份额也可分为如下三部分:按经营单位所在地为贵州省的出口货物的价值量部分、贵州省外的中国大陆省份以及境外通过流入贵州省所“间接出口”或“引致出口”部分、贵州省产出的增加值部分所带来的出口,该份额为三个部分的代数和。
用数学符号表示为:
 (2.10) (2.10)
此证明可结合(2.1)式和(2.9)式即可,证明从略。
3.定理3(贵州省政府应承担增值税出口退税的份额定理)考虑不同产品的税率和征收增值税时的财政体制后,贵州省应承担的出口退税的税额计算问题
(2.9)式只是测算了应由贵州省承担出口退税的货物价值量问题,要计算贵州省应承担的出口退税额,还需要解决三个问题:第一,了解各种产品(利用投入产出分析时,有时用部门表示或转换)的退税率,如农业的出口退税率我们用农产品的出口退税率,而建筑业、运输业、其他服务业的出口退税率为零(因为建筑业、运输业等的流转税是营业税而非增值税),等等。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


