论文导读::证据理论自提出后。神经网络的评价机理。以便能对铅锌企业低碳生产水平进行实证评价。迫切需要建立一套铅锌企业低碳化生产水平的评价模型。
论文关键词:DS证据理论,BP神经网络,铅锌企业低碳生产水平,评价
1引言
自2003年英国政府首次提出建设“低碳社会”之后,“低碳经济”、“工业转型”等与低碳发展模式有关的问题就开始成为理论界研究的热点,特别是2009年9月爆发国际金融危机以后,人们对低碳发展模式的关注更是广泛而深刻。复旦大学环境经济研究中心李志青[1]认为低碳发展模式是“后危机时代”的实体经济发展模式的方向与出路,鲍健强[2]等也认为“以低能耗、低排放、低污染为特征的低碳发展模式是未来经济发展模式的新选择”。在2010年6月举行的第十三届中国北京国际科技产业博览会中国高新企业发展国际论坛上,与会专家学者一致认为,后金融危机时代引导全球经济走出低谷的是低碳经济,低碳发展模式是企业未来发展的方向。除此以外,清华大学齐晔教授等[3]-[10]也对低碳发展模式的实质、中国人均碳排放的影响因素、地区碳排放与经济发展水平和能源消耗强度的关系及城市低碳经济发展综合评价指标体系等方面进行了比较深入的研究。无可否认节能减排论文,在全球气候变暖的背景下,以低能耗、低污染、低排放为基础的低碳发展模式成为全球热点,这一场由欧美发达国家掀起的“低碳革命”已在全球悄然进行,“低碳发展”也几乎冲击了全球所有的企业,铅锌企业作为传统的“高碳”行业,其面临的压力更大。据我们课题组的实证调查,我国90%左右的产品是用严重污染环境的烧结法工艺生产的,落后的竖罐炼锌工艺不仅没有淘汰,反而在西部地区还在进一步发展,铅的生产过程对环境的破坏也十分严重[11]。因此,在低碳经济背景下,迫切需要建立一套铅锌企业低碳化生产水平的评价模型,以便能对铅锌企业低碳生产水平进行实证评价,从而发现铅锌企业低碳化发展过程中的不足,促进铅锌企业的低碳可持续发展。本文将首先分析了基于“DS-BP”方法的评价机理,然后运用DS证据理论结合BP神经网络法得出一个铅锌企业低碳生产水平的评价模型,最后对该模型进行实证研究。
2 基于“DS-BP”方法的评价机理
2.1传统方法的挑战---有效证据的融合和处理问题
查阅相关的文献可以看到,在一些比较有效评价方法中,AHP法主要是基于一种比较各因素的相对重要度的思想来进行评价的节能减排论文,它的最大的优点是可以处理定性和定量相结合的问题,可以将决策者的主观判断与政策经验导入模型,并加以量化处理,但是AHP方法也同时也具有很大的局限性,例如过度依赖专家,同时需要数据源不能存在“亦此亦彼”的模糊问题;在运用传统AHP方法对不完全信息多属性决策问题进行决策时,决策者给出的判断矩阵常常含有残缺元素(称残缺判断矩阵),AHP法不能解决称残缺判断矩阵问题核心期刊目录。对于第一个问题,Fuzzy方法通过引进因素集U能较好地解决各指标因素不能存在“亦此亦彼”的模糊性问题,但对判断矩阵含有残缺元素的不完全信息多属性决策问题依然无法解决,不能区分“亦此亦彼”和“不知道”的差异。DS证据理论则在度量和合成不确定性信息方面有着独特的优势,DS证据理论自提出后,广泛用于研究不确定性问题的求解。
在实际的评价过程中,因为不同指标的权重也不相同,同时不同专家由于其专业知识和工作背景不同,对不同评价指标所赋予的权重具有差异,而且有时差异较大,因此必须寻求一种能对他们有价值信息进行融合的方法。不仅如此,作为被测变量的企业低碳生产水平的高低本身也是一个相对模糊的概念,其影响因素也同样具有不准确性、不完整性和不确定性,这“三性”使得AHP、Fuzzy等评价方法同时遇到挑战,而证据理论和神经网络理论确能很好地对这一问题加以改善。下面节能减排论文,具体分析一下证据理论和神经网络理论对“不准确性、不完整性和不确定性”问题改善的机理,从而为模型的构建奠定基础。
2.2 DS证据理论融合证据的机理
Dempster和Shafer在20世纪70年代提出的D-S证据理论[12]是对概率论的扩展,他们一方面在证据理论中引入了一种能够区分不确定和不知道之间差异的信任函数,以克服AHP、Fuzzy等的理论局限,另一方面,D-S证据理论通过放松贝叶斯方法对统一辨识框架、完整的先验概率和条件概率等约束条件,使得该理论既可以对互相相容的命题进行证据融合,也可以对相互重叠、非互不相容的命题进行证据融合,这样,D-S证据理论在评价领域中的应用空间得到了极大的拓展。随后,Strat T M.[13],Beynon M J,Curry B,MorganPH[14],Malcolm Beyond[15],Smets P[16]等也对证据理论的研究作出了重要的贡献。证据理论的评价机理主要有以下三个相关方面的内容。
2.1.1证据理论中证据融合的三个基本函数
证据理论的三个基本函数是证据理论的基础,在证据融合中扮演着重要的角色。设有一个判决问题,对于该问题所能认识到的所有可能结果用有限集合Ω表示,那么人们所关心的任一命题对应于Ω的一个子集,所有这些子集的集合称为判别框,它包括有限个互不相容的命题或者说元素,记为(u1,u2,u3,……,ui)。设U为判别框架,对于U有2Ω是Ω的幂集,则可定义U的基本概率赋值函数(Basic ProbabilityAssignment Function,简写为满足:
 BPAF)m:2U[0,1],满足: BPAF)m:2U[0,1],满足:
 
命题U为U的非空子集节能减排论文,称为焦元,m(A)称为基本概率赋值,它表示对命题A的精确信任程度,表示对A的直接支持。基本概率赋值函数是一个[0,1]之间的正数,它与支持某一假定的证据相联系,其大小表示该证据支持或反对该假定的精确程度,通常用m(A)表示。m(A)表示提供给A的基本可信度,而不是对A的总信度。若A≠Ω,则m(A)表示对A的信任程度,若A=Ω,则m(A)表示m这个数没有赋予任一子集上,没有提供信息。
 对于判别框Ω上的基本概率赋值函数m,如果有函数Bel: 2Ω[0,1]满足: 对于判别框Ω上的基本概率赋值函数m,如果有函数Bel: 2Ω[0,1]满足:

则称所定义的函数Bel为Ω上的信任函数 (Belief Function),Bel(A)表示对命题A的总信任程度。
 设判别框Ω上的函数Pl: 2Ω [0,1]满足: 设判别框Ω上的函数Pl: 2Ω [0,1]满足:

则称所定义的函数Pl(A)为似然度函数(Plausibility Function),Pl(A)表示对不否定命题A的信任度,是所有与A相交的集合的基本概率赋值之和。
信任函数可以理解为证据对A的总支持度,似然度函数pl(A)表示不否定的信任程度,是支持A的总的信任最大值。信任函数Bel与基本概率赋值函数BPAF是互相唯一确定的核心期刊目录。似然度函数表示不否定A的信任度,并以PL(A)-Bel (A)表示对A未知即不确定的程度。
2.1.2证据理论中信息不确定性的表示
DS证据理论最大的特点就是可以很好地表示未知信息的程度,在证据理论中,[Bel(A),Pl(A)] 称为命题A的信任度区间,[0,Bel(A)]表示命题A支持证据区间,[0,Pl(A)]表示命题A的拟信区间,[Pl(A),1]表示命题A的拒绝证据区间,Pl(A)- Bel(A) 为命题A的不确定度节能减排论文,其值反映了对命题A 的“未知”信息,该差值越小,则表明“未知”成分越小,证据对假设的支持越明确。
2.1.3 证据理论中证据融合的方法
对于同一判别框,根据不同的证据信息,会得到不同的信度函数,如果这些证据是相互独立的,利用证据理论中证据的融合法则就可以计算出一个信度函数作为这几个证据联合作用下产生的信度函数,这样就可以利用这些信息提高对事件的置信度。
 设Bel1, Bel2, ……,Beln是同一判别框上由相互独立的证据信息产生的信度函数,m1,m2,……mn,是对应的基本概率赋值函数,如果 设Bel1, Bel2, ……,Beln是同一判别框上由相互独立的证据信息产生的信度函数,m1,m2,……mn,是对应的基本概率赋值函数,如果 ,那么由下式定义的函数m:2Ω[0,1]是基本概率赋值函数: ,那么由下式定义的函数m:2Ω[0,1]是基本概率赋值函数:
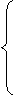 0( 0( ) )
M(A) = K ( ( ) )
-1
 其中K= 1 - 其中K= 1 -
1/3 1 2 3 下一页 尾页 |


