论文导读::身份乘客评价综合得分。下文将采取主成分分析和因子分析法。主成分分析和因子分析原理[1]。
论文关键词:京津高铁,乘客评价,主成分分析,因子分析
一、基本研究目的
在调研过程中我们发现,不同乘客对京津城际高铁有不同的诉求,总体来说有:降低票价、改进购票方式、灵活班次、改善车上环境、实现转乘、完善周边设施;同时,京津城际铁路还有着自身的优点,如:速度快、班次多、环境舒适。同时,京津城际高速铁路还具有方便短程出行和旅游的特殊竞争优势。
如此之多的影响因素综合作用下,乘客究竟会做出何种选择?为了进一步探究不同身份的乘客对京津城际铁路的选择倾向,并用尽可能简单的变量判断和解释不同身份乘客的选择,下文将采取主成分分析和因子分析法,利用SPSS16.0软件,对不同身份的乘客的选择进行判断和预测。
二、主成分分析和因子分析原理[1]
(一)主成分分析的含义:
主成分分析是用原来指标重新组合成一项新的互相无关的综合指标来代替原指标,并根据实际需要从中选取几个较少的综合指标来代替原来指标,以达到简化数据的目的。这些指标可以尽可能多的反应原始数据的信息,这种统计方法就是主成分分析或主分量分析。
(二)、主成分分析的基本思想:
选取对原变量做线性组合后方差较大的几个量(这些变量反映的信息是最完全的)交通论文,这些综合指标称为主成分,主成分之间不相关,且方差递减。
(三)、主成分分析的几何意义:
p个变量组成p维空间,而n个样品就是p维空间中的n个点,做线性变换,将 构成的坐标系旋转产生新的坐标系,新坐标轴使之通过样品的最大方差的方向。此时主成分问题就是寻找p维空间的椭球体的主轴问题。形象的说,以二维主成分为例,由横纵坐标来代表,基于数据的二维正态分布假定,这些样本数据在这个坐标上形成一个椭圆形的点阵。在极端情况下,椭圆的长轴上尽可能多的集中了变化的数据,而短轴方向上数据变化极少。那么主成分就由二维降到一维了。对于多维的情况,变量就形成了一个P维空间的椭球体免费论文下载。那么找到多维椭球体的主轴和相应能最大限度反应信息的最长的几个轴,就达到了主成分分析的目的。 构成的坐标系旋转产生新的坐标系,新坐标轴使之通过样品的最大方差的方向。此时主成分问题就是寻找p维空间的椭球体的主轴问题。形象的说,以二维主成分为例,由横纵坐标来代表,基于数据的二维正态分布假定,这些样本数据在这个坐标上形成一个椭圆形的点阵。在极端情况下,椭圆的长轴上尽可能多的集中了变化的数据,而短轴方向上数据变化极少。那么主成分就由二维降到一维了。对于多维的情况,变量就形成了一个P维空间的椭球体免费论文下载。那么找到多维椭球体的主轴和相应能最大限度反应信息的最长的几个轴,就达到了主成分分析的目的。
(四)、主成分分析的数学模型:
将原始资料库  ( ( )做线性组合: )做线性组合:

上述线性方程组应满足如下条件:
1)、 , ,
2)、 线性无关,即两辆协方差为零,这是为了使得第二个主成分中不再含有第一组成分已经说明了的重复性息。 线性无关,即两辆协方差为零,这是为了使得第二个主成分中不再含有第一组成分已经说明了的重复性息。
3)、方差依次递减
如果指标数据的量纲不同,需要先对原始数据进行标准化处理。由于本文的所有样品均为被调查者频数,故不需要进行标准化数据。
(五)、因子分析的基本思想:
因子分析是通过对变量的相关系数矩阵内部结构的研究,找出能控制所有变量的少数几个变量去描述多个变量之间的相关关系。这少数几个变量就称之为因子。根据相关性的大小把变量分组,使得同组内的变量之间的相关性较高,不同组内的相关性较低。
因子分析分为R型因子分析和Q型因子分析。R型因子分析是对变量进行分析从相关系数矩阵出发,而Q型因子分析从相似系数矩阵出发,对样本进行分析。
(六)、因子分析的数学模型:
R型因子分析【2】

简记为:
满足下列条件:
1、
2、 ,即各因子不相关且同方差 ,即各因子不相关且同方差
 ,即各个特殊因子不相关且异方差。 ,即各个特殊因子不相关且异方差。
其中F是表示因子列向量,是 的共有向量交通论文,成为公公因子。 的共有向量交通论文,成为公公因子。 称为因子载荷,是第i个变量在第j个因子上的负荷,他表示 称为因子载荷,是第i个变量在第j个因子上的负荷,他表示 在坐标轴 在坐标轴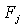 上的投影。 上的投影。 是不能被公公因子包含的量,成为特殊因子。 是不能被公公因子包含的量,成为特殊因子。
因子分析的目的就是通过模型 以F代替X,由于 以F代替X,由于 故达到了简化模型的目的【3】。 故达到了简化模型的目的【3】。
二、调研数据收集
根据连续五次的跟踪调研数据,发现有超过90%的乘客认为京津高铁对旅游的促进作用非常大,因此选取京津城际高铁的“短途旅游优势”为变量之一,并采取科学的方法定量描述这一指标;选取乘客出行乘坐列车最关注的几个问题为其它城际高铁服务质量的评价指标,包括:速度、班次,乘车环境;同时,通过调研收集的数据分析,选取价格、购票方式、班次的灵活性、灵活转乘以及周边配套设施等指标,对乘客的态度进行评价。调研数据显示,乘客的身份有:公务员、学生、企业人员、工人、农民、科研教育人员等。将数据计算、整合,为分析做好准备。
三、进行主成分分析和因子分析,得出结论
定义矩阵: 其中 其中 代表不同的职业的乘客, 代表不同的职业的乘客, 代表不同的出行时间。将数据输入SPSS16.0如下: 代表不同的出行时间。将数据输入SPSS16.0如下:
对城际高铁所体现出来的短期旅游优势的定性数据进行分析,化为可以和其他乘客诉求和高铁自身优点同时进行运算的指标。

  通过AnalyzeData Reduction Factor进行主成分分析,得到方差贡献率表。表示各个主成分在方差中所占比例的大小,是主成分贡献大小的标志,也是主成分得以存在的判别基础。 通过AnalyzeData Reduction Factor进行主成分分析,得到方差贡献率表。表示各个主成分在方差中所占比例的大小,是主成分贡献大小的标志,也是主成分得以存在的判别基础。
|
Total Variance Explained
|
|
Component
|
Initial Eigenvalues
|
Extraction Sums of Squared Loadings
|
|
Total
|
% of Variance
|
Cumulative %
|
Total
|
% of Variance
|
Cumulative %
|
|
1
|
2.794
|
69.852
|
69.852
|
2.794
|
69.852
|
69.852
|
|
2
|
1.180
|
29.509
|
99.361
|
1.180
|
29.509
|
99.361
|
|
3
|
.025
|
.623
|
99.984
|
|
|
|
|
4
|
.001
|
.016
|
100.000
|
|
|
|
其中的Initial Eigenvalues是四个指标的主轴长度,是样品相关系数矩阵的特征值。前两个主成分的积累已达总方差的99%以上,之后的主成分解释作用微乎其微。
由于在操作的时候选择的提取主成分的判定准则是特征值大于1,方差贡献率达到80%以上,即:
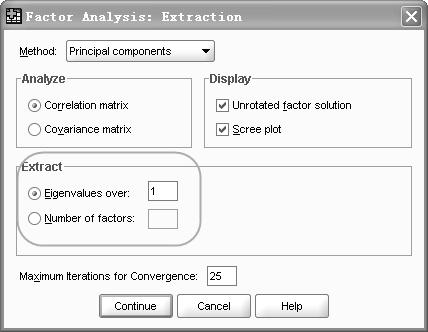
故累计的方差贡献率还可以通过碎石图判断出来:
(其中纵轴表示方差贡献率)

通过载荷矩阵的输出结果,可以看出前两个主成分表示为各个原变量的线性组合的系数,也是主成分和相应原变量的相关系数,相关系数越大交通论文,表示主成分对原变量的代表性越强免费论文下载。
|
Component Matrixa
|
|
|
Component
|
|
1
|
2
|
|
工作日
|
.708
|
.699
|
|
周末
|
.933
|
.347
|
|
短期假期
|
.938
|
-.344
|
|
长期假期
|
.736
|
-.673
|
即:

以载荷阵的系数除以主成分特征值对应的平方根即可得到三个主成分中的每个指标对应的系数,写出主成分的表达式:

以相应的方差贡献率在两个主成分中的总方差贡献率中的比重为权,得到的结果作为所需的高铁短程旅游优势的新变量【4】:
写出新变量的表达式:

带入相应的 的数据即可得到新指标的值: 的数据即可得到新指标的值:
|
企业人员
|
193.225
|
|
学生
|
112.214
|
|
工人
|
34.413
|
|
科研教育人员
|
42.831
|
|
公务员
|
38.839
|
|
农民
|
29.814
|
于是,与其他高铁的优势和乘客的诉求合并在一起,得到新的数据矩阵:

由于此时量纲已经不再完全一致,所以要首先对变量进行标准化处理,再接着进行因子分析。
下表是因子旋转后的载荷阵,可以明显的看出两个公共因子将指标分为两类
1/2 1 2 下一页 尾页 |


