图7 试样断裂后的开裂角
Fig.7 the crack angle of the specimen
|
（3）当冻深为110cm时，取距表层土60cm深的冻土体，制备Ⅱ型裂纹试样，控制试验温度为-3.1℃,含水量为17%，获得非线性断裂韧度 值。如表1所示。这个结果相应于土体从冻结开始到2005年1月20日的冻结历史。
表1 原状冻土的Ⅱ型非线性断裂韧度试验计算结果
Tab.1 theexperimental results of nonlinear fracture toughness for frozen soil
|
编号
|
裂纹长度（cm）
|
试样尺寸（cm）
|
临界荷载
|
等效剪切力
|
非线性断裂韧度
|
开裂角
|
|
|
|
|
|
|
|
|
|
|
KT-1
|
4.32
|
39.9
|
9.7
|
11.2
|
8.33
|
2.78
|
56.69
|
61
|
|
KT-2
|
4.17
|
42.4
|
10.4
|
9.8
|
6.11
|
2.04
|
24.61
|
64
|
|
KT-3
|
4.02
|
39.3
|
11.1
|
9.6
|
9.47
|
3.16
|
41.92
|
65
|
|
KT-4
|
4.69
|
41.3
|
10.4
|
10.8
|
8.27
|
2.76
|
57.71
|
78
|
|
KT-5
|
4.11
|
39.5
|
9.9
|
10.2
|
9.07
|
3.02
|
61.01
|
55
|
|
KT-6
|
4.26
|
41.0
|
10.2
|
10.5
|
8.07
|
2.69
|
53.37
|
58
|
|
KT-7
|
4.34
|
41.5
|
11.3
|
10.3
|
5.33
|
1.78
|
14.19
|
49
|
|
KT-8
|
4.35
|
41.1
|
10.4
|
10.0
|
4.67
|
1.56
|
12.61
|
52
|
（3）按修正因子法计算结果
对上述试样同时做出了 曲线，并用修正因子法计算出非线性断裂韧度，结果列于表2中。
表2 原状冻土的Ⅱ型非线性断裂韧度 试验计算结果
Tab.2 the calculate value ofnonlinear fracture toughness forfrozen soil
|
编号
|
裂纹长度
|
临界荷载
|
等效剪切力
|
表观应力强度因子
|
修正因子
|
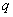
非线性断裂韧度
|
|
KT-1
|
4.32
|
8.33
|
2.78
|
0.095
|
0.89
|
0.153
|
|
KT-2
|
4.17
|
6.11
|
2.04
|
0.065
|
0.86
|
0.103
|
|
KT-3
|
4.02
|
9.47
|
3.16
|
0.084
|
0.896
|
0.136
|
|
KT-4
|
4.69
|
8.27
|
2.76
|
0.097
|
0.928
|
0.16
|
|
KT-5
|
4.11
|
9.07
|
3.02
|
0.1
|
0.936
|
0.166
|
|
KT-6
|
4.26
|
8.07
|
2.69
|
0.086
|
0.849
|
0.135
|
|
KT-7
|
4.34
|
5.33
|
1.78
|
0.048
|
0.876
|
0.077
|
|
KT-8
|
4.35
|
4.67
|
1.56
|
0.052
|
0.912
|
0.085
|
非线性断裂韧度 与非线性能量释放率值都是表征冻土材料的非线性特征，二者应有对应关系。对于线弹性情况，能量释放率 与断裂韧度 有如下关系：
 （15）
假定上述关系对非线性情况也同样成立，若取－3℃时的 ＝400MPa， ＝0.25，则将换算为实验研究，并与实测比较，除两个试样误差较大，其余的基本是一致的，其结果列在表3中。
表3 将换算为与实验测得的相对比的结果
Tab.3 the comparisonbetween the value of calculatedform andthe value of formthe experiment
|
试样编号
|
|
换算的
|
实测的
|
误差
|
|
KT-1
|
0.153
|
55.07
|
56.69
|
2.94%
|
|
KT-2
|
0.103
|
24.84
|
24.61
|
0.94%
|
|
KT-3
|
0.136
|
43.38
|
41.92
|
3.37%
|
|
KT-4
|
0.16
|
60.23
|
57.71
|
4.19%
|
|
KT-5
|
0.166
|
64.67
|
61.01
|
5.66%
|
|
KT-6
|
0.135
|
42.91
|
53.37
|
24.39%
|
|
KT-7
|
0.077
|
13.82
|
14.19
|
2.70%
|
|
KT-8
|
0.085
|
16.96
|
12.61
|
25.66%
|
5.结论
（1）本文的研究是针对沈阳地区的土质所进行的原状冻土断裂力学试验。由于冻土工程中经常发生剪切的破坏形式，所以着重对Ⅱ型断裂（剪切）破坏的四点弯曲直裂纹试样进行了实验研究。并用染色剂对裂纹尺寸采用着色法观测。通过对当地土质进行分层冻胀量的观测，得出不同埋深处的冻胀量、冻融的关系，并以此来严格控制试样制作、试验时的温度，对原状冻土的Ⅱ型非线性应变能量释放率和非线性断裂韧度进行测试研究，这是对原状冻土非线性断裂力学试验的进一步的探索和尝试，它为今后进一步的研究工作奠定了基础。
（2）本文给出了关于冻土的两种非线性断裂韧度测试方法的结果，分别是基于能量平衡的测试方法和基于修正因子的测试方法，在实际工程应用中，可以相互参照，灵活运用。
（3）由于原状冻土完全处于自然状态下，其结构及内部缺陷随机性较大，实验过程中所采集的数据有一定的离散性，因此需要更多的试样和大量的实验数据，并进行统计分析，使结果与实际情况相符。
参考文献
[1]吴紫汪，马巍.冻土强度与蠕变[M]。兰州：兰州大学出版社，1994。(WuZ W, Ma W. Frozen soil strength and creep[M]. Lanzhou, Lanzhou UniversityPress.)
[2]李洪升，朱元林.冻土断裂力学及其应用[M]。北京：海洋出版社，2002.（Li H.S., Zhu Y.L, FractureMechanics of Frozen Soil and Its Application[M]. Beijing, China Ocean Press. 2002.）。
[3]李洪升，刘增利，朱元林。冻土断裂韧度测试的理论和方法[J]。岩土工程学报，2000，22（1）：61-65。(Li H.S., Liu Z L, Zhu Y.L. Theory and methods on testsof the fracture toughness K_(Ⅰc) of frozen soil[J]. Chinese Journalof Geotechnical Engineering, 2000，22（1）：61-65.)
[4]Wang Yuedong，Li Hongsheng，Liu XiaoZhou. The experiment research of nonlinear mode Ⅱ fracturetoughness for the original state frozen soil，the 11thexperimental mechanics conference of china，2005：377-386
[5]王铎.断裂力学[M]，南宁：广西人民出版社，1982，74-76。(Wang F. Fracture Mechanics[M]. Nanning: Guangxi PeoplePress.)
[6]Hillerborg.A,modeer.M, Petersson.P.E, Analysis of crack formation and crack growth inconcrete by means of fracture mechanics and finite elements, Cement andConcrete Research, 1976, 773-782
[7]Xu, X-P andNeedleman, A. Numerical simulations of fast crack growth in brittle solids,Journal of the Mechanics and Physics of Solids, Vol. 42, pp. 1397-1434 (1994).
[8]WhittakerB.N., singhand R.N. Sun G. [M]. Rock Fracture Mechanics. Elsevier SciencePublishers B.V. 1992.
3/3 首页 上一页 1 2 3 |
