| 浅谈“握手问题”的运用
论文关键词:“握手问题”,运用
问题 1 某班共有n名学生,在元旦班级联欢晚会上两两握手致意,那么他们共握手多少次?
对这个问题,我们可以作这样的假设:第1个学生分别与其他(n-1)个学生握手,可握(n-1)次手;第2个学生也分别与其他(n-1)个学生握手,可握(n-1)次手;一依此类推,第n个学生与其他(n-1)个学生握手,可握(n-1)次手,如此共有n×(n-1)次握手,显然此时每两人之间都握了两次手进行计算的.因此,按照题意,n个人每两人之间握一次手共握了  次手.这样解决问题,我们不妨称它为“握手问题”. 次手.这样解决问题,我们不妨称它为“握手问题”.
“握手问题”在数学上的应用。现举几例如下:
例1 已知1条直线上共有6个点,那么这条直线上共有几条线段?
分析 将6个点看作是6名学生,每两点构成一条线段,就好比是2个学生握手.而6个学生两两握手时.按照“握手问题”,共握了  次手,从而直线上5个点共构成15条线段. 次手,从而直线上5个点共构成15条线段.
例2 经过同一个端点的10条射线,这10条射线可以组成几个角?
分析 经过同一个端点的10条射线就好像10个学生,每2射线可以组成一个角,就好像是2个学生握1次手,其中n=10,按照“握手问题”,共可画  条直线. 条直线.
例3 一个n边形,共有多少条对角线?n边形的所有对角线与它的各边共形成多少个三角形?
分析:从n边形的一个顶点出发有 条对角线,n个顶点共有 条对角线,n个顶点共有 条对角线,但有重复的情况,故有 条对角线,但有重复的情况,故有 条对角线;n边形的所有对角线与它的各边共有 条对角线;n边形的所有对角线与它的各边共有 条线段,任意一条线段与另外 条线段,任意一条线段与另外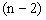 个顶点形成 个顶点形成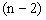 个三角形, 个三角形, 条线段形成 条线段形成 个三角形,但对于一个 个三角形,但对于一个 来说,重复算了三次,故共形成 来说,重复算了三次,故共形成  个三角形 个三角形
问题2 某班同学毕业时都将自己的照片向全班其它同学各送一张表示留念,全班共有n个人,那么全班一共送了多少张照片?
分析:送照片的时候,你送我一张,我也要送你一张。一个人送 张,n个人既全班送 张,n个人既全班送 张。这类问题有握手问题相似,但它不需要除以2。 张。这类问题有握手问题相似,但它不需要除以2。
下面几个例子,在使用握手问题是不用除2.
例4某列火车在甲、乙两城市间来回行驶,除甲、乙两城市外,中间还停靠7个站点,那么该列火车共需准备多少种票价?多少种车票?
分析 该题中,火车从A站点到B站点的车票与从B站点到A站点的票价是不一样的,所以按照“握手问题”考虑问题时,不需要除2,,火车在甲、乙两城市间来回行驶共有9个站。则共需准备 种车票. 种车票.
例5 实验中学初一(1)班学生临时元旦,每人都互送明信片一张,现已知该班有60名同学,那么共需多少张明信片?
分析 该问题中,甲同学送给乙同学的明信片与乙同学送给甲同学的明信片不一样,因此按照“握手解法”考虑问题时,不需除以2,即该班共需60×59=3540张明信片.
问题3 甲、乙两个篮球队比赛结束后,与对方互相握手,以示友好,已知每个球队有5个队员,则他们共可握多少次手?
分析 甲球队的每个队员分别与乙球队的5个队员握手,可握5次手,而甲球队有5个队员,所以共握5×5=25次手.
引申: 如果甲球队有m个队员,乙球队有n个队员,则可握mn次手,像这样解决问题的方法,我们也称它为“握手问题”.
例6 已知由边长为1的正方形拼成如图所示的长方形ABCD,图中共有(1) 多少个矩形? (2)图中有几个正方形? A D
B C
分析(1)图1中AD上有5个点,可得AD上有  个线段;AB上有4个点, 可得AB上有 个线段;AB上有4个点, 可得AB上有 =6个线段.而AD上的任一 条线段与线段AB上任一线段“握手”,都会构成一个距形,所以图中 =6个线段.而AD上的任一 条线段与线段AB上任一线段“握手”,都会构成一个距形,所以图中
中共有mn =10×6=60个矩形.
(2)AD上线段与AB上线段“握手”时构成正方形,就要求“握手”的两条线段必须相等。如下表
线段 线段长度度
AB上条数
AD上条数
正方形个数
1
3
4
4×3=12
2
2
3
333 3×2=6
3
1
22
2 2×1=2
由表中可得“握手”12+6+2=20次,即图中共有20个正方形,
上面三种类型的题型,我们在具体应用的时候要认真分析题目,正确的选择握手解法。
|


