 , ,  ∩ ∩  等,都是完备空间A的子集。 等,都是完备空间A的子集。
关于上述时空结构形态拓扑集的小结。A是一个(可以是整个自然界,也可以是具体物体的或确定空间物质分布的)时空结构形态全集,并对应一个现实世界的拓扑空间(A,A ),A的最小组成单元(粒子)用 表示,即 A =﹛ai︱1≤ i≤∞﹜,拓扑空间(A,A )的任何一个子集可能对应一个现实世界的某个物体的一个特定的时空结构形态,该特定的时空结构形态可以通过无穷尽的吸收或放射同样为时空结构形态的光量子集,变换出该物体的所有宏观现实状态;拓扑空间同类态之间的差集是光量子集,任何单一同类时空结构形态的补集是光量子集!光量子态充斥在整个空间中,是统计量子,是现实世界的场媒,是现实世界变化的“时间因子”,同时对于一个稳定物态,光量子场媒的能量密度为α T4 ,波谱分布为类正则分布。(参考,宋太伟,《光子的本质》,《时空结构几何》)。 表示,即 A =﹛ai︱1≤ i≤∞﹜,拓扑空间(A,A )的任何一个子集可能对应一个现实世界的某个物体的一个特定的时空结构形态,该特定的时空结构形态可以通过无穷尽的吸收或放射同样为时空结构形态的光量子集,变换出该物体的所有宏观现实状态;拓扑空间同类态之间的差集是光量子集,任何单一同类时空结构形态的补集是光量子集!光量子态充斥在整个空间中,是统计量子,是现实世界的场媒,是现实世界变化的“时间因子”,同时对于一个稳定物态,光量子场媒的能量密度为α T4 ,波谱分布为类正则分布。(参考,宋太伟,《光子的本质》,《时空结构几何》)。
2.2.3.2 多粒子体系时空结构形态集的层次边界、能态关系,混乱度
由定理 2可知,多粒子体系的粒子能量ε大小随粒子的同类时空结构态(简并态)的数量mШ的增大而增大,内能密度u 随同能同类时空结构态总集的态数量MШ的增大而增大。本节进一步解析MШ的内在逻辑关系,及MШ和u、T的逻辑关系。
多粒子体系,通过不断光热(拓扑)变换,可以演化出不同的宏观状态。关于非平衡态的问题,有重要现实意义的主要包括相变、自组织等,将在下一章重点论述,这里主要论述与探讨稳态下的相关问题。
复杂物体可能由多态多结构组成,涉及到物体内部不同组织结构的交汇边界问题,有了结构边界,物体大小与形状描述即更为具体、精确。时空结构理论对边界的定义如下:
定义 6 物态边界:宏观稳态下两个不同物态的空间结构形态集的交汇区间集。
物态边界实质上是两种不同空间结构的过渡区间,也可以理解为是一种空间结构的外沿区,是有“厚度”的。一般为非空开集,不属于两种物态集中任一个物态集的边界混合集。
假设两种相邻物态集分别为A、B,交汇边界态集为C,三者的关系是:
A+B ⊇ A∪B ⊃ C,且:C ⊄A ,A ∩C ≧∅,C ⊄ B, B ∩C ≧∅。只有当C =∅空集时,空间几何意义上,为一个几何界面。
复杂物体,内部可能会分为多个不同物态区域,在均衡条件下,温度相等,结构属性、内能密度、空间大小等不同。
同一物态下的时空结构形态总集,直接由最小稳定粒子单元的时空结构形态子集,按照一定的拓扑变换条件,进行变化组合,最为简单。稳态下,任意空间大小的多粒子包络的时空结构形态子集的u、T都是确定并相等的,即拓扑变换存在标度不变性。也就是说,粒子的运动状态在统计意义上是相同的,这是前文论述的稳定同态粒子的运动内能统计平均值 确定并相同的另一种解释。 确定并相同的另一种解释。
一个基本粒子单元的时空结构形态,实质反映的是粒子运动形态,包含了一切物理运动属性(经典物理中用自由度表征),如运动空间(束缚作用、结构势)、动量、旋量、电磁性等。统计意义上,只考虑集合体系的平均运动属性及关系,主要是与热运动能ε相关的物理性质及对应关系。根据前文,粒子的热运动能ε,随对应的同能同类时空结构态(简并态)的数量mШ的增大而增大。热运动能ε的粒子的简并态的数量mШ,显然与粒子的运动空间成正比(与有序束缚势能成反比),同时正比于其它对能级大小几无贡献的旋量自由度等。按照一定模型可以计算出单粒子能级与简并态数量的关系(13)式mШ= f(ε/β)。考虑到平均结构势能,这里的能级为ε-µ,-µ为单粒子受到的平均约束势场(有序能),ε为单粒子运动能级(无序能,统计能部分,ε-µ实为单粒子的总能级)。
假设复杂多态多粒子体系,均衡稳定下温度为T,存在I个不同空间结构态区域,每个单一状态区域内包含Ji种不同的最小粒子单元,单一i状态区域内的同一种j最小粒子单元的个数为Nij,Kiju为单一i状态区域内的Nij个同一种j最小粒子单元在总能级u保持不变条件下各个粒子单元的能级组合数,则复杂系统整体的空间结构形态数MШ的一般关系为:
MШ=  MШi = MШi = 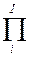  MШij = MШij =    (45) (45)
在均衡稳态下,单态区域时空拓扑变换存在标度不变性,任意空间大小的多粒子包络体的时空结构形态子集的内能密度与温度都是确定并相等的,单态区域内任意空间大小的多粒子包络体的最小粒子单元的不同能级组合态,以所有最小粒子单元能级均取相同的平均能级
 为最大态、最可能态。(45)中 为最大态、最可能态。(45)中
11/30 首页 上一页 9 10 11 12 13 14 下一页 尾页 |


