将式代入式并分离实部和虚部,可以得到四个方程,将它们整理化简,得到 , , , , , , 的表达式,在这些表达式中考虑稳态响应解的条件,即 的表达式,在这些表达式中考虑稳态响应解的条件,即

经化简消去 和 和 后最终得到关于 后最终得到关于 和 和 的两个方程如式所示,其中 的两个方程如式所示,其中 , ,

式中 , , 0和 0和 中含有参数 中含有参数 , , , , 及变量 及变量 、 、 的高次方项。给定不同参数,可求得对应幅频曲线,求解时应将 的高次方项。给定不同参数,可求得对应幅频曲线,求解时应将 利用 利用 转化成激振力频率 转化成激振力频率 。 。
图10~13给出了不同速度下第一阶模态和第二阶模态的幅频特性曲线,由于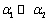 ,而 ,而 和 和 在同一量级,故图中分别用 在同一量级,故图中分别用 和 和 来表示第一、二阶模态的幅值。从图10~11可以看出,当 来表示第一、二阶模态的幅值。从图10~11可以看出,当 时,第一、二阶模态分别有六组解,由于所取的解均为正数,故这六组解在同一相平面内。一阶模态的第5、6组解所对应的曲线中,幅值随频率增加而增大,二阶模态的对应曲线则恰恰相反。此外,两图中的第4组解也表现出相反的特性,这三组解都体现了两阶模态幅值大小的相互转换,是非线性系统内共振的特有规律。第1、2组解对应的曲线变化规律相同,虽然不能说明内共振现象,但从本文后面的稳定性研究中可以看到,这两组解大多数为不稳定解。 时,第一、二阶模态分别有六组解,由于所取的解均为正数,故这六组解在同一相平面内。一阶模态的第5、6组解所对应的曲线中,幅值随频率增加而增大,二阶模态的对应曲线则恰恰相反。此外,两图中的第4组解也表现出相反的特性,这三组解都体现了两阶模态幅值大小的相互转换,是非线性系统内共振的特有规律。第1、2组解对应的曲线变化规律相同,虽然不能说明内共振现象,但从本文后面的稳定性研究中可以看到,这两组解大多数为不稳定解。

图10 时 时 的幅频特性曲线 的幅频特性曲线
Fig.10Amplitude-frequencycurvesof with with

图11 时 时 的幅频特性曲线 的幅频特性曲线
Fig.11Amplitude-frequencycurvesof with with
从图12~13中看出,在 的条件下,第一、二阶模态的四组解所对应的曲线均表现出了相反的变化规律,内共振现象非常显著。从图10~13的整体比较来看,当速度由 的条件下,第一、二阶模态的四组解所对应的曲线均表现出了相反的变化规律,内共振现象非常显著。从图10~13的整体比较来看,当速度由 增加到 增加到 时,第一、二阶模态的幅值都由六个解变为四个解,共振区域明显减小,同时,幅值减小。 时,第一、二阶模态的幅值都由六个解变为四个解,共振区域明显减小,同时,幅值减小。
在 、 、 、 、 时,做出 时,做出 和 和 下的 下的 、 、 响应曲线(图略)。其形式与图8~9相同,也表现为随着频率的变化,幅值交替增减,能量在两阶模态之间相互传递,证明了内共振现象的存在。 响应曲线(图略)。其形式与图8~9相同,也表现为随着频率的变化,幅值交替增减,能量在两阶模态之间相互传递,证明了内共振现象的存在。

图12 时 时 的幅频特性曲线 的幅频特性曲线
Fig.12Amplitude-frequencycurvesof with with

图13 时 时 的幅频特性曲线 的幅频特性曲线
Fig.13Amplitude-frequencycurvesof with with
图14给出了不同激振力幅值下的幅频特性曲线,由于对一、二阶模态的影响相似,故文中只列出了 的幅频特性曲线(以下同),由图中可知,激振力的增大,使共振区扩大,振幅增加,同时,发生内共振的频率逐渐远离第一阶固有频率。当 的幅频特性曲线(以下同),由图中可知,激振力的增大,使共振区扩大,振幅增加,同时,发生内共振的频率逐渐远离第一阶固有频率。当 时,产生了幅值封闭曲线,说明此时非线性对幅值的增大加以限制。 时,产生了幅值封闭曲线,说明此时非线性对幅值的增大加以限制。

图14 , , , , , , 的 的 幅频特性曲线 幅频特性曲线
Fig.14Amplitude-frequencycurvesof with with
图15给出了不同阻尼下的幅频特性曲线,由图可知,随着阻尼的增大,振幅减小,共振区域也变小,且更快产生幅值封闭曲线,但总体来说,阻尼对近似解的影响并不显著。

图15 , , , , , , 的 的 幅频特性曲线 幅频特性曲线
Fig.15Amplitude-frequencycurvesof with with , , , , , ,
图16给出了不同小参数下的幅频特性曲线,由图中可知,小参数 对幅频特性曲线基本没有影响。 对幅频特性曲线基本没有影响。

图16 , , , , , , 时 时 幅频特性曲线 幅频特性曲线
Fig.16Amplitude-frequencycurvesof with with
考虑到解的稳定性分析的重要性,本文利用李雅普诺夫一次近似判别理论对多尺度法共振解的稳定性进行了初步研究。将式代入式并分离实部和虚部,整理化简后可以变形表示为式,其 矩阵 矩阵 是关于 是关于 的函数,把幅频特性曲线上每一点的 的函数,把幅频特性曲线上每一点的 值同时代入矩阵 值同时代入矩阵 的特征方程,可求得对应的特征值,并运用稳定性定理判断该点的稳定性。 的特征方程,可求得对应的特征值,并运用稳定性定理判断该点的稳定性。

图17给出了 , , , , 条件下的第一、二阶模态幅频特性曲线的稳定点和不稳定点。 条件下的第一、二阶模态幅频特性曲线的稳定点和不稳定点。 3/4 首页 上一页 1 2 3 4 下一页 尾页 |


