
图2零初值下的 幅频特性曲线 幅频特性曲线
Fig.2Amplitude-frequencycurvesof withzeroinitialvalue withzeroinitialvalue

图3 的幅频特性曲线 的幅频特性曲线
Fig.3Amplitude-frequencycurvesof

图4 和 和 幅频特性曲线的比较 幅频特性曲线的比较
Fig.4Differencebetween and and
图5为圆柱壳在不同轴向运动速度下的完整幅频特性曲线。由图可知,在第一阶固有频率附近均存在跳跃现象,随着速度减小,非线性现象更加明显,多值区越来越复杂并出现新的曲线,响应幅值也相应增大。

图5 时 时 的幅频特性曲线 的幅频特性曲线
Fig.5Amplitude-frequencycurvesof with with
图6为圆柱壳在不同激振力振幅下的完整幅频特性曲线。由图中可知,随着激振力振幅的增大,幅频特性曲线的非线性特征越来越明显,第一、二阶模态的耦合程度加强,即内共振现象越发显著。
图7为圆柱壳在不同阻尼下的完整幅频特性曲线。由图中可知,随着阻尼的减小,幅频特性曲线的幅值增加,共振频率的偏移程度减小,非线性特征越来越明显,内共振现象也越发显著。

图6 时 时 的幅频特性曲线 的幅频特性曲线
Fig.6Amplitude-frequencycurvesof with with

图7 时 时 的幅频特性曲线 的幅频特性曲线
Fig.7Amplitude-frequencycurvesof with with
为进一步证实上述幅频特性曲线中所表明的内共振现象的存在,现对相同条件下的响应曲线进行研究。图8和图9分别是 ,阻尼 ,阻尼 0,速度 0,速度 条件下, 条件下, 和 和 时 时 和 和 响应曲线,图中的两个模态幅值交替增减,能量在它们之间相互传递,再一次证明文中所选两阶模态间存在内共振现象。 响应曲线,图中的两个模态幅值交替增减,能量在它们之间相互传递,再一次证明文中所选两阶模态间存在内共振现象。

图8 时 时 , , 的响应 的响应
Fig.8Responseof and and with with

图9 时 时 , , 的响应 的响应
Fig.9Responseof and and with with
3多尺度法分析1:1内共振
通过前面数值计算中得到的结果 , , ,并令模态方程组中的第1、3式 ,并令模态方程组中的第1、3式 ,第2、4式 ,第2、4式 ,则式可简化成两个方程,引进摄动小参数 ,则式可简化成两个方程,引进摄动小参数 后,这两个方程可写为 后,这两个方程可写为


其中, , , , , , , 为陀螺项的系数, 为陀螺项的系数, , , , ,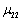 , ,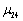 为阻尼项的系数。系统所对应的两阶固有频率 为阻尼项的系数。系统所对应的两阶固有频率 , , 由方程得出,同时可得振型系数 由方程得出,同时可得振型系数 , ,


令 ,将其看成不同时间尺度的自变量,并将解的精度取为 ,将其看成不同时间尺度的自变量,并将解的精度取为 ,则解可设为 ,则解可设为

将 代入式,可推出 代入式,可推出 和 和 的一、二阶导数的形式为 的一、二阶导数的形式为

其中, 。 。
将式和代入和,令 和 和 同次幂的系数相等,得到0和1阶偏微分方程组 同次幂的系数相等,得到0和1阶偏微分方程组
 : :

 : :

系统中 和 和 彼此并不独立,由数值解知两阶模态之间存在内共振,设方程的解为 彼此并不独立,由数值解知两阶模态之间存在内共振,设方程的解为

其中,cc表示前面表达式的复共轭。第一阶固有频率 接近第二阶固有频率 接近第二阶固有频率 ,很可能发生1:1内共振,设 ,很可能发生1:1内共振,设

其中, 和 和 为频率调谐参数。把式和代入式方程组的右边并整理得 为频率调谐参数。把式和代入式方程组的右边并整理得

其中 ~ ~ 是关于 是关于 , , , , , , , , , , 的函数,因此设 的函数,因此设 和 和 含有如下形式特解 含有如下形式特解

把式代入式的左边并整理,由 和 和 两边的系数相等可以列出四个方程,根据它们所组成的非齐次方程组的解的条件可以进一步得到另外四个方程,考虑到本文研究的激振力频率在第一阶固有频率的附近,并且关于小参数的展开也在第一阶固有频率附近,故选择采用其中的两个方程进行计算 两边的系数相等可以列出四个方程,根据它们所组成的非齐次方程组的解的条件可以进一步得到另外四个方程,考虑到本文研究的激振力频率在第一阶固有频率的附近,并且关于小参数的展开也在第一阶固有频率附近,故选择采用其中的两个方程进行计算

方程是关于 , , , ,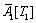 , , 的函数,设 的函数,设

其中 和 和 是系统分别以 是系统分别以 和 和 振动时第一阶模态和第二阶模态的幅值。 振动时第一阶模态和第二阶模态的幅值。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


