而权重 的积分可以表示为 的积分可以表示为
 (10) (10)
如果变异函数为高斯型变异函数并且不考虑块金效应( ),则变异函数的积分为 ),则变异函数的积分为
 (11) (11)
其中 是误差函数 是误差函数
 (12) (12)
从式(9)-(11)就可以得到用已知点的函数值来估计未知函数的积分近似。在随机变量 的均值和方差计算中代入其近似的密度函数 的均值和方差计算中代入其近似的密度函数 并用基于克里金方法的积分近似表达 并用基于克里金方法的积分近似表达
 (13) (13)
其中 是一个选取的常数,满足 是一个选取的常数,满足
 (14) (14)
 是一个小的参数,它取决于计算中精度的要求,文中取 是一个小的参数,它取决于计算中精度的要求,文中取 。 。
3、数值模拟
3.1随机性的反问题中的基本假设
两点假设:
1)细观参数随机量唯一性假设:
假设复合材料性能宏观随机性只由一种细观随机性引起,也就是只有一个细观随机变量起作用,如组份材料弹性模量或泊松比或微结构的随机性,而且这个随机变量是可以确定的。
2)随机量正态分布假设:
假设描述复合材料宏观有效性能随机性的随机变量和组分性能的细观随机变量都是正态分布的,这样就将问题简化为已知描述宏观有效性能随机性正态分布的均值与方差,反推出引起宏观随机性的细观随机变量正态分布的均值与方差。
3.2迭代程序的步骤
在反问题中由已知描述宏观有效性能随机性的正态分布的均值( )与均方差( )与均方差( ),采用迭代的方法,逼近真实的细观随机变量正态分布的均值( ),采用迭代的方法,逼近真实的细观随机变量正态分布的均值( )与均方差( )与均方差( )物理论文,以下介绍迭代程序的主要流程: )物理论文,以下介绍迭代程序的主要流程:
1) 时第一步迭代,细观随机变量正态分布的均值 时第一步迭代,细观随机变量正态分布的均值 与方差 与方差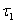 取为 取为 。通过克里金的随机分析方法计算复合材料的宏观有效性能的均值 。通过克里金的随机分析方法计算复合材料的宏观有效性能的均值 和均方差 和均方差 ,与 ,与 和 和 比较,决定下一步迭代的取值cssci期刊目录。如果 比较,决定下一步迭代的取值cssci期刊目录。如果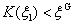 ,第二步迭代的均值 ,第二步迭代的均值 取为 取为 ,相反 ,相反 时,取为 时,取为 ;第二步迭代的均方差 ;第二步迭代的均方差 也类似选取。 也类似选取。
2) 时,由细观随机变量的均值 时,由细观随机变量的均值 与均方差 与均方差 采用克里金的随机分析方法计算复合材料的宏观有效性能的均值 采用克里金的随机分析方法计算复合材料的宏观有效性能的均值 和均方差 和均方差 。如果 。如果 ,令 ,令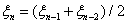 ;并且用 ;并且用 代替 代替 ;如果 ;如果 , , ,令 ,令 ;如果 ;如果 , , ,令 ,令 ;第 ;第 步迭代的均方差 步迭代的均方差 也类似选取。 也类似选取。
3)对于给定的正数 和 和 用于控制迭代结束的精度。如果当迭代到 用于控制迭代结束的精度。如果当迭代到 步时, 步时, 且 且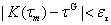 时物理论文,迭代收敛并结束,此时 时物理论文,迭代收敛并结束,此时 和 和 就认为是真实的细观随机变量正态分布的均值 就认为是真实的细观随机变量正态分布的均值 与均方差 与均方差 的近似。如果对于给定整数 的近似。如果对于给定整数 ,当迭代次数大于 ,当迭代次数大于 时,迭代仍不收敛,迭代也结束,需要重新选取控制精度来计算。 时,迭代仍不收敛,迭代也结束,需要重新选取控制精度来计算。
3.3模拟结果分析
考虑单向纤维增强复合材料,在体积份数 时,通过实验测得复合材料的纵向弹性模量 时,通过实验测得复合材料的纵向弹性模量 的均值与均方差,计算中用到的其它数据列于表1,通过这些数据反推出假设服从正态分布的纤维弹量模量的均值 的均值与均方差,计算中用到的其它数据列于表1,通过这些数据反推出假设服从正态分布的纤维弹量模量的均值 与均方差 与均方差 。单向纤维增强复合材料中纤维分布取为四边形分布[15]。 。单向纤维增强复合材料中纤维分布取为四边形分布[15]。
表1:材料性能与控制精度参数
|
|
纤维
|
基体
|
|
弹性模量(GPa)
|
未知正态分布:
|
4.5
|
|
泊松比
|
0.2156
|
0.39
|
|
均值 GPa ,均方差 GPa ,均方差 GPa GPa
|
|
 GPa, GPa,  GPa, GPa, 
|
: Material propertyand parameters of controlled resolution
table1图1、图2分别给出了随着迭代次数变化时物理论文,计算的单向纤维增强复合材料的纵向弹性模量的均值与方差cssci期刊目录。这两个图中的红线分别表示实验测得的均值与方差,而数据点表示迭代中由选取的纤维弹性模量均值与方差而计算得到的整个复合材料纵向弹性模量的均值与方差。从这两个图可以看到迭代过程收敛较快,当 时计算结果已经满足表1中的精度要求。 时计算结果已经满足表1中的精度要求。
2/3 首页 上一页 1 2 3 下一页 尾页 |


