论文导读::建立非均匀材料宏观力学性能与微结构参数之间的定量关系一直是人们所关心的问题,利用材料微结构参数和组分性能预报复合材料宏观力学性能,已经取得了很大的进展,然而已知复合材料宏观性能,如何开展组分性能的随机识别,目前的研究工作还不多见。本文考虑了复合材料的随机性,在已知复合材料宏观有效性能的随机性条件下,采用克里金随机分析方法,对复合材料组分性能的随机性进行识别,通过单向纤维复合材料的宏观有效性能的随机性,计算得到了纤维弹性模量的均值与方差,证明了该方法的有效性。
论文关键词:均匀化方法,复合材料,力学性能,随机识别
1、绪论
微观力学的研究不仅仅是通过组元材料性能理论预报宏观材料性能,还有一个很重要的目的是根据微结构的不均匀性确定物理量和力学量在微观层次上局部场的涨落和分布情况的变化,目前预报复合材料有效性能的方法和模型很多,如根据体积份数和夹杂的几何尺寸及组分性能来推导有效性能的自洽法[1-3]、广义自洽法[4、5]和M–T法[6–8]等,上述方法虽然建立起了复合材料的微观量与宏观量的关系,但不能给出局部场的细节。70年代出现了被称为Asymptotic HomogenizationTheory的方法物理论文,即均匀化理论[9],用于分析两个或更多个长度尺度的物理系统,是一套严格的数学理论。该方法用均质的宏观结构和非均质的具有周期性分布的微观结构描述原复合材料结构:将力学量表示成关于宏观坐标和微观坐标的函数,并用微观和宏观两种尺度之比为小参数展开,用摄动技术将原问题化为微观均匀化问题和宏观均匀化问题,对这些问题的求解给出了具有微观非均质结构的复合材料的有效性能,并给出了非均质扰动的复合材料的微观应力场。然而,复合材料由于组份材料性能的随机性或微结构的不确定性会引起整个复合材料宏观上有效性能的不确定性cssci期刊目录。Marcin Kaminski[10]和Sakata等[11-12]利用基于摄动的均匀化方法考虑了材料微结构不确定性,对纤维增强复合材料进行三维的随机性分析,得到了有效性能的统计特性。侯善芹、刘书田[13]对随机颗粒分布的复合材料,应用均匀化方法预测了材料的宏观等效弹性性能,研究了其统计特性,探讨颗粒大小、分布和几何形状的变化对材料等效弹性性能的影响。
实际上物理论文,在复合材料生产和应用中,往往只是通过一些实验得到了复合材料宏观有效性能的统计特征,而不清楚这种宏观随机性到底如何受组分材料性能随机性和微结构不确定的影响,因此由已知的宏观性能随机性的统计特征反推出未知的组份材料性能的随机性或微结构的不确定性,对于材料设计和工艺改进具有重要的理论意义和实用价值。本文就是基于上述思想,考虑了复合材料的随机性,在已知复合材料宏观有效性能的随机性条件下,结合地质统计学的克里金方法[14],发展了一种基于克里金的随机分析方法,运用均匀方化方法对随机复合材料的有效性能进行了预报[15],通过反向迭代的思想对复合材料组分材料性能随机性进行了识别。
2、克里金随机分析方法
2.1密度函数的克里金近似
如果随机变量 、 、 关系可以用一个未知函数 关系可以用一个未知函数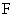 来表示,即 来表示,即
 (1) (1)
假设随机变量 、 、 的概率密度分别为 的概率密度分别为 、 、 ,则存在关系 ,则存在关系
 (2) (2)
在复合材料宏观有效性能预报的均匀化方法中物理论文,均匀化系数或复合材料有效性能(相当于随机变量 )应是组分材料性能和单胞几何形状(相当于随机变量 )应是组分材料性能和单胞几何形状(相当于随机变量 )的函数,在组份材料性能和单胞几何形状为已知的随机变量时,如果可以知道联系着随机变量 )的函数,在组份材料性能和单胞几何形状为已知的随机变量时,如果可以知道联系着随机变量 、 、 的函数 的函数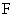 或 或 ,就可以得到整个复合材料性能随机分布的情况。然而这种函数关系 ,就可以得到整个复合材料性能随机分布的情况。然而这种函数关系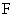 很难得到,并且 很难得到,并且 不能直接解析的表达出来。在这种情况下,我们可以采用有限差分的形式来近似 不能直接解析的表达出来。在这种情况下,我们可以采用有限差分的形式来近似 。 。
 (3) (3)
随机变量 的均值 的均值 和方差 和方差 可以表示为 可以表示为
 (4) (4)
应用普通的克里金方法,随机变量 在随机变量 在随机变量 位置为 位置为 处,普通克里金估计值 处,普通克里金估计值 可以写成 可以写成
 (5) (5)
其中 是普通克里金方法中的权重, 是普通克里金方法中的权重,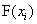 是在位置 是在位置 处的观察值或计算值。由式(2)可以得到随机变量 处的观察值或计算值。由式(2)可以得到随机变量 的密度函数 的密度函数 的近似 的近似
 (6) (6)
上式中 可以通过代入式(5)变化为 可以通过代入式(5)变化为
 (7) (7)
其中 cssci期刊目录。 cssci期刊目录。
如果变异函数为已知,假设是高斯型变异函数,则可以求得 的解析形式: 的解析形式:
 (8) (8)
其中 。根据式(7)就可以得到随机变量 。根据式(7)就可以得到随机变量 密度函数近似的显式表达式 密度函数近似的显式表达式 ,它是关于变量 ,它是关于变量 的显式表达。 的显式表达。
2.2基于克里金的积分近似
为了计算式(4)的积分,一些数值积分方法可以采用物理论文,比如说辛普森积分方法等,本文中采用基于克里金方法的积分近似。假设被积分函数 用离散采样点 用离散采样点 来近似表达 来近似表达
 (9) (9)
1/3 1 2 3 下一页 尾页 |


