 (23) (23)
其中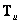 为 为 阶矩阵, 阶矩阵, 为 为 处未知状态向量。由(23)式可求出结构的自由振动方程: 处未知状态向量。由(23)式可求出结构的自由振动方程:
 (24) (24)
上式的解为复数,故定义固有频率和损耗因子为[2]: ; ; . .
2.2部分覆盖ACLD板的动力学分析
部分带状覆盖ACLD板可沿 方向分为3段,如图4所示。第1段和第3段未敷设ACLD(光板),其控制方程为(14)式;第2段为敷设了ACLD的层合板,其控制方程为(19)式。 方向分为3段,如图4所示。第1段和第3段未敷设ACLD(光板),其控制方程为(14)式;第2段为敷设了ACLD的层合板,其控制方程为(19)式。
在边界点 和 和 处,由齐次扩容精细积分法[8],状态向量之间有下列关系: 处,由齐次扩容精细积分法[8],状态向量之间有下列关系:
 , ,  , ,  (25) (25)
其中: 、 、 和 和 分别为1、2、3段的传递矩阵, 分别为1、2、3段的传递矩阵, 、 、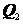 和 和 是由外荷载引起的非齐次项。 是由外荷载引起的非齐次项。
令 , 其中 , 其中 , ,  ,则(25)式中的第二式可改写为: ,则(25)式中的第二式可改写为:
 (26) (26)
由(25)式中的第一、第三式和(26)式消掉 和 和 ,可求出部分带状覆盖ACLD板起点和终点的传递关系: ,可求出部分带状覆盖ACLD板起点和终点的传递关系:
 (27) (27)
3 数值分析
为了验证本文方法的正确性,考虑一个四边简支的全覆盖ACLD板,几何和物理参数如下[2]:   . .
表1 自由频率和损耗因子与文献值的比较
|
模态
(m, n)
|
频率
|
损耗因子
|
|
本文值
|
文献值
|
本文值
|
文献值
|
|
1,1
|
113.2
|
113.4
|
0.0926
|
0.0844
|
|
1,2
|
224.1
|
224.8
|
0.0476
|
0.0473
|
|
2,1
|
311.2
|
311.1
|
0.0355
|
0.0352
|
|
2,2
|
421.5
|
422.1
|
0.0262
|
0.0265
|
Nature frequency and loss factor comparison between the Reference
table1表1为本文方法所计算出来的自由频率和损耗因子与文献[2]中计算结果的比较,由表中可以看出,两者吻合得较好,特别是自由振动频率,误差均小于1%. 由此可见,本文所建立的力学模型具有较高的精度。
考虑一对边简支,另一对边为悬臂约束条件的正方形ACLD板, ,其余参数与上例相同,令位移和速度增益系数 ,其余参数与上例相同,令位移和速度增益系数 ,取自由端中点 ,取自由端中点 为反馈点,当固定端产生位移 为反馈点,当固定端产生位移 时,点 时,点 的位移频响函数如图5所示,其中频响函数定义为: 的位移频响函数如图5所示,其中频响函数定义为: . 为了比较ACLD板的减振效果,图中还画出了PCLD板和光板的频率响应曲线。由图中可以看出,敷设约束层阻尼后,结构的共振自由频率略有增加,位移大幅减小,特别是在共振峰值处,其位移幅值可减小数十倍。可见,约束层阻尼是一种非常有效的减振手段论文怎么写。由图中还可以看出,PCLD结构和ACLD结构的共振频率几乎是相同的,即引入压电作动力对结构的频率影响不大。但由于压电作动力的作用,ACLD对于振动的抑制更为显著,特别是在较低的频率范围内。图6为粘弹性层厚度 . 为了比较ACLD板的减振效果,图中还画出了PCLD板和光板的频率响应曲线。由图中可以看出,敷设约束层阻尼后,结构的共振自由频率略有增加,位移大幅减小,特别是在共振峰值处,其位移幅值可减小数十倍。可见,约束层阻尼是一种非常有效的减振手段论文怎么写。由图中还可以看出,PCLD结构和ACLD结构的共振频率几乎是相同的,即引入压电作动力对结构的频率影响不大。但由于压电作动力的作用,ACLD对于振动的抑制更为显著,特别是在较低的频率范围内。图6为粘弹性层厚度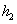 分别为 分别为 时的频率响应曲线。在本文的结构参数情况下,随着粘弹性层厚度的增加,结构的减振效果反而逐渐减弱。因此,在ACLD板的结构设计时,粘弹性层的厚度的增加并不一定能够增强减振的效果。 时的频率响应曲线。在本文的结构参数情况下,随着粘弹性层厚度的增加,结构的减振效果反而逐渐减弱。因此,在ACLD板的结构设计时,粘弹性层的厚度的增加并不一定能够增强减振的效果。
考虑一个带状部分覆盖正方形ACLD板物理论文, ,其余物理和几何参数与上例相同。ACLD结构长度分别为 ,其余物理和几何参数与上例相同。ACLD结构长度分别为 ,对称敷设在板的中部时的频率响应曲线如图7所示。由图中可知,在大多数频率范围内,随着覆盖长度的增加,位移逐渐减小。但在部分频段内,部分覆盖的减振效果却优于全覆盖方式,这说明全覆盖敷设并不一定能够获得最好的减振效果。令覆盖长度 ,对称敷设在板的中部时的频率响应曲线如图7所示。由图中可知,在大多数频率范围内,随着覆盖长度的增加,位移逐渐减小。但在部分频段内,部分覆盖的减振效果却优于全覆盖方式,这说明全覆盖敷设并不一定能够获得最好的减振效果。令覆盖长度 ,图8给出了 ,图8给出了 时,频率响应的变化。由图中可知,速度增益系数越大,振动抑制的效果越好。在频率较低时,三条曲线的区别尤为明显,随着频率的增加,差别逐渐。 时,频率响应的变化。由图中可知,速度增益系数越大,振动抑制的效果越好。在频率较低时,三条曲线的区别尤为明显,随着频率的增加,差别逐渐。
4 结论
同时考虑压电材料的正、逆压电效应,本文建立了ACLD板的机电耦合模型,并提出了一种应用广泛,具有较高精度的半解析方法。数值分析表明,压电约束层在低频范围能更有效地抑制结构的振动,提高结构的阻尼性能。但在较高频段内,它的减振效果并不明显。文中还分析了粘弹性层厚度等参数对ACLD板的振动和阻尼特性的影响。研究表明,ACLD板的动力学特性受各种因素的影响,其变化规律较为复杂,通过进一步优化结构参数,有望得到更好的减振性能,这也是我们下一步研究的重点问题。
VIBRATIONAND DAMPING ANALYSES ON A LAMINATED PLATE WITH ACTIVE CONSTRAINED LAYER DAMPING
Jing Lu1,2** YuyingHuang1 Yu Xiang2
(1 College of Civil Engineering andMechanics, Huazhong University of Science and Technology, Wuhan, 430074)
(2 Department of Automotive Engineering, Guangxi University ofTechnology, Liuzhou, 545006)
Abstracts: Employing the constitutive relations of the piezoelectricmaterials, the membranes induced by the piezoelectric effect is derived. Onlytaking into account the shearing deformation in the viscoelastic core, andaccording to the thin plate theory and linear theories of viscoelasticmaterials, we established the integrated first order differential equations ofa laminated plate treated with active constrained layer damping under theboundary of simply supported at two opposite edges. On the basis of the presentmodel, a semi-analytical method is proposed by combing with extendedhomogeneous capacity precision integration technology and superposition method.The influence of the structural parameters on the dynamic characteristics of a laminatedplate with active constrained layer damping plate is also discussed in thepaper.
Keywords: active constrainedlayer damping; plate; first order differential equations; vibration, damping
3/4 首页 上一页 1 2 3 4 下一页 尾页 |


