 (11) (11)
其中 和 和 分别表示位移和速度增益系数。 分别表示位移和速度增益系数。
将 沿y方向用Fourier级数展开,并将电压表达式代入(10)式后可得: 沿y方向用Fourier级数展开,并将电压表达式代入(10)式后可得:
 (12) (12)
式中, , , 为 为 的Fourier展开系数。 的Fourier展开系数。
对于有一对边简支(沿x轴方向)的矩形板,也可将位移和内力分量沿y轴展开为Fourier级数,将(9)式和(12)式代入矩形薄板的平衡方程、几何方程和物理方程,经整理并无量纲化后可导出指定波数n下压电层的一阶控制方程:
 (13) (13)
式中,上标(3)表示约束层, , , 为方程的无量纲状态向量。其中, 为方程的无量纲状态向量。其中, , , , ,  , , 为任意长度, 为任意长度, 为板的薄膜刚度。为了简化书写,推导中省略了上标 为板的薄膜刚度。为了简化书写,推导中省略了上标 . .  为系数矩阵,各元素表达式见附录。 为系数矩阵,各元素表达式见附录。 , , 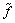 和 和 分别表示外激励和层间作用力的幅值, 分别表示外激励和层间作用力的幅值, , ,  . .
同理可求出基板的一阶控制方程:
 (14) (14)
其中,无量纲状态向量为 ,载荷向量为 ,载荷向量为 ,将基板的几何和物理参数代入 ,将基板的几何和物理参数代入 的表达式即可求出约束层的系数矩阵 的表达式即可求出约束层的系数矩阵 . .
由于(13)和(14)式中的层间作用力未知,方程不能直接求解,本文利用粘弹性层的位移连续性条件和法向平衡方程解决这一问题,进而得出ACLD板的整体控制方程。
1.3 ACLD板的整合一阶状态方程 ACLD板的整合一阶状态方程
对于粘弹性层,仅考虑它的剪切变形,根据一阶剪切变形理论和层间连续条件,并结合胡克定律可求出粘弹性层中面的剪应力的幅值:

(15)
式中, 表示粘弹性层的剪切模量, 表示粘弹性层的剪切模量, 分别表示基板、粘弹性层和约束层的厚度。因此,(13)和(14)式中切向的层间作用力可写为: 分别表示基板、粘弹性层和约束层的厚度。因此,(13)和(14)式中切向的层间作用力可写为:
 (16) (16)
由图2可知,粘弹性层中面的剪应力还会在压电约束层和基板中面产生偏心力矩,将该力矩转化为法线方向的克希霍夫等效剪力:
 (17) (17)
式中, 分别表示基板和约束层中面到粘弹性层中面的偏心距, 分别表示基板和约束层中面到粘弹性层中面的偏心距,  . .
由图3可求出粘弹性层的法向平衡方程:
 (18) (18)
其中, 为粘弹性层的密度。 为粘弹性层的密度。
将载荷表达式代入(13)和(14)式,并利用(18)式消去层间的法向相互作用力 ,经整理后可求出ACLD板的12阶状态方程,与进行Fourier展开和无量纲化后的(8)式联立,最终可导出ACLD板的整合一阶状态方程: ,经整理后可求出ACLD板的12阶状态方程,与进行Fourier展开和无量纲化后的(8)式联立,最终可导出ACLD板的整合一阶状态方程:
 (19) (19)
式中,系数矩阵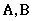 为14阶方阵,各元素的具体表达式详见附录。 为14阶方阵,各元素的具体表达式详见附录。 为整合的状态向量, 为整合的状态向量,  为外载荷向量, 为外载荷向量, 为广义的单位压电作动力向量。 为广义的单位压电作动力向量。
2 数值计算方法
2.1耦合方程的求解
由于在非齐次项中包含了反馈点的位移 ,(19)式为耦合方程,直接求解非常困难。但是,外载荷向量 ,(19)式为耦合方程,直接求解非常困难。但是,外载荷向量 和单位压电作动力向量 和单位压电作动力向量 的数值是已知的,它们单独作用时的状态方程可以用齐次扩容精细积分法[9]解出。因此,根据叠加原理,任意点的位移可以表示为: 的数值是已知的,它们单独作用时的状态方程可以用齐次扩容精细积分法[9]解出。因此,根据叠加原理,任意点的位移可以表示为:
 (20) (20)
式中物理论文, 分别表示由 分别表示由 单独作用在点 单独作用在点 处所引起的位移。令 处所引起的位移。令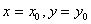 ,代入(20)式后即可求出反馈点的位移: ,代入(20)式后即可求出反馈点的位移:
 (21) (21)
将求出的 代入(19)式,再次利用齐次扩容精细积分法即可求出各点的状态向量。 代入(19)式,再次利用齐次扩容精细积分法即可求出各点的状态向量。
自由振动时外载荷为零,(19)式变为一阶齐次常微分矩阵方程,利用精细积分法可求出起点和终点状态向量之间的关系:
 (22) (22)
式中, 为 为 阶传递矩阵。通常,在边界 阶传递矩阵。通常,在边界 和 和 上分别存在7个已知的边界条件和7个未知的边界条件,代入(22)式经移项整理后可得: 上分别存在7个已知的边界条件和7个未知的边界条件,代入(22)式经移项整理后可得:
2/4 首页 上一页 1 2 3 4 下一页 尾页 |


