X  = = , ,
是极大,从而P也在此时达到极大.
定理证毕.
2 任意多项和的线性极小问题的推广
2.1 几个引理
引理5[1] 如果n个正变数X1 、X2 、X3 ……Xn的积是定值,那么他们的和,当这些数相等时是极大.
引理6[1] 如果n个正变数X1 、X2 、X3 ……Xn的积是定值k,那么和A1 X1+ A2 X2 +A3 X3+……+AnXn,当A1 X1=A2 X2 =A3 X3=……=AnXn时是极小,其中系数A1 、A2、 A3 …… An以及k都是给定的正常数.
引理7[1] 如果积X1x X2 x X2 x X3x X3x 是定值,其中X1 、X2 、X3是正变数,而指数x 是定值,其中X1 、X2 、X3是正变数,而指数x 、x 、x 、x 、x 是给定的正有理数,那么和X1 +X2 +X3,当变数X1 、X2 、X3同指数x 是给定的正有理数,那么和X1 +X2 +X3,当变数X1 、X2 、X3同指数x 、x 、x 、x 、x 成比例时是极小. 成比例时是极小.
引理8[1] 设积X1x X2 x X2 x X3x X3x 是定值k,其中X1 、X2 、X3是正变数,而指数x 是定值k,其中X1 、X2 、X3是正变数,而指数x 、x 、x 、x 、x 是给定的正有理数,那么和A1X1+A2 X2 +A3 X3 ,当 是给定的正有理数,那么和A1X1+A2 X2 +A3 X3 ,当 = = = = 时是极小,其中A1 、A2、 A3 都是正数. 时是极小,其中A1 、A2、 A3 都是正数.
2.2 主要推广结果
定理3 如果积X1x X2 x X2 x X3x X3x ……Xnx ……Xnx 是定值,其中X1 、X2 、X3 ……Xn是正变数,而指数x 是定值,其中X1 、X2 、X3 ……Xn是正变数,而指数x 、x 、x 、x 、x ……xn是给定的正有理数,那么和X1 +X2 +X3 +……+Xn ,当变数X1 、X2 、X3 ……Xn同指数x ……xn是给定的正有理数,那么和X1 +X2 +X3 +……+Xn ,当变数X1 、X2 、X3 ……Xn同指数x 、x 、x 、x 、x ……xn成比例时是极小. ……xn成比例时是极小.
证明 假设
S=X1 +X2 +X3 +……+Xn , (3)
X1x X2 x X2 x X3x X3x ……Xnx ……Xnx =k, =k,
其中k是给定的正数.
因为x 、x 、x 、x 、x ……xn可能是正整数也可能是正分数,但考虑正整数亦可表示成正分数的情形,因此把x ……xn可能是正整数也可能是正分数,但考虑正整数亦可表示成正分数的情形,因此把x 、x 、x 、x 、x ……xn变成有最小公分母D的分数: ……xn变成有最小公分母D的分数:
x = = , x , x = = , x , x = = , …… , xn= , …… , xn= , ,
于是(3)变为:
S=  + +  + +  +……+ +……+  , ,
即:
S=x  + x + x  + x + x  +……x +……x  , ,
即:
S= + + + + +……+ +……+ , ,
于是和S成为x + x + x + x + x +……x +……x 项的和,这些项的积 项的和,这些项的积
 + + + + +……+ +……+
= ( ) ) ( ( ) )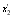 ( ( ) ) ……( ……( ) ) , ,
是定值,等于 , ,
因此,由引理事知,和S 当 = = = = =……= =……= 时, 时,
即: = = = = =……= =……= 时是极小. 时是极小.
定理证毕.
定理4 设积X1x X2 x X2 x X3x X3x ……Xnx ……Xnx ,是定值k,即: ,是定值k,即:
X1x X2 x X2 x X3x X3x ……Xnx ……Xnx =k, =k,
其中X1 、X2 、X3 ……Xn是正变数,而指数x 、x 、x 、x 、x ……xn是给定的有理数,那么和 ……xn是给定的有理数,那么和
A1 X1+A2 X2 +A3 X3+ ……+An Xn ,当 = = = = =……= =……= 时极小, 时极小,
其中A1 、A2、 A3 、…… An都是正常数.
证明 事实上,设x = =  , x , x = =  , x , x = =  ,……,x ,……,x = =  , ,
那么积X  X X  X X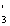  …… X …… X  是定值: 是定值:
X  X X  X X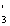  …… X …… X  =( =( )k, )k,
因而由定理3知,和X +X +X + X + X +……X +……X , 当 , 当 = = = = =……= =……= 时极小. 时极小.
定理证毕.
3 线性极大极小问题的互逆性的推广
引理9[1] 设f(X1 、X2 、X3), g(X1 、X2 、X3)是正变数X1 、X2 、X3的二个函数,A是一个给定的数,若当X1 、X2 、X3在条件
2/3 首页 上一页 1 2 3 下一页 尾页 |


