(3)当 时,对应方程 时,对应方程 有两个不同的根,需要进一步讨论 有两个不同的根,需要进一步讨论 。这一块主要讨论两点:① 。这一块主要讨论两点:① 之间的大小关系;② 之间的大小关系;② 是否在定义域或题目条件指定的区域中。这一部分运算往往比较繁琐,讨论容易出现混乱,解答时思路要清晰,还要有耐心。 是否在定义域或题目条件指定的区域中。这一部分运算往往比较繁琐,讨论容易出现混乱,解答时思路要清晰,还要有耐心。
解答这类问题时,要严格按照上面的步骤和要求,有序进行,解答的过程才能更加全面
和彻底,不会有遗漏中国学术期刊网。
仿照例3,按上述的步骤和要求,再来训练一个题目,
例4:已知函数 ,求函数 ,求函数 在区间 在区间 上的最小值。 上的最小值。
分析:需要确定函数 在区间 在区间 上的单调性,按步骤进行。 上的单调性,按步骤进行。
解:第一步:确定函数 的定义域,求导函数 的定义域,求导函数 ,并将 ,并将 转化成用二次函数来表示。 转化成用二次函数来表示。
函数 的定义域为 的定义域为 , ,
设 ,则 ,则 , ,
第二步:讨论二次函数 的判别式 的判别式 。 。
因为这里的 恒大于等于0,所以不需要再讨论,直接求出方程 恒大于等于0,所以不需要再讨论,直接求出方程 的根: 的根:
第三步:讨论 之间的大小关系, 之间的大小关系, 是否在区间 是否在区间 上。 上。
 , , 时, 时,
 当 当 时, 时, 对任意 对任意 恒成立,此时 恒成立,此时 对任意 对任意 也恒成立二次函数, 也恒成立二次函数,
∴ 在区间 在区间 上单调递增,∴ 上单调递增,∴
 当 当 时, 时,
若 时,则 时,则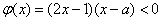 ,此时 ,此时
若 时,则 时,则 ,此时 ,此时
∴ 在区间 在区间 上单调递减,在区间 上单调递减,在区间 上单调递增, 上单调递增,
∴
 当 当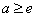 时, 时, 对任意 对任意 恒成立,此时 恒成立,此时 对任意 对任意 也恒成立, 也恒成立,
∴ 在区间 在区间 上单调递减,∴ 上单调递减,∴
综上可得:  时, 时, ; ;
 时, 时,
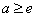 时, 时,
第三步可以通过绘制草图或列表格来辅助完成。
面对这一类型的题目时,不要轻易放弃,只要按照上述的步骤和要求依次执行,问题便可以得到解决。如果时间允许的话,可以在草稿纸上列出解答问题的提纲,这样解题的思路会更加清晰。解答的过程中,还要注意书写的规范,不同层次的分类讨论,最好用上不同的序号(如 , , , , …或①,②,③…)加以区分。 …或①,②,③…)加以区分。
3/3 首页 上一页 1 2 3 |


