论文导读::当利用导数来判断含参数函数的单调性时,问题往往会变得复杂,运算也会变得繁琐。其解答过程中会蕴含着几个层次的分类讨论,当它们叠加在一起的时候,需要我们有很好的分析问题和解决问题的能力,同时还需要有一定的耐心。本文从例题出发,对解决这一类问题的步骤进行了探讨和总结。对其中会出现的一些问题,也相应的给出了解决的方法。
论文关键词:参数单调性,分类讨论,二次函数,判别式,方程的根
导数是研究函数的重要工具,而利用导数来判断函数的单调性也是高考重点考查的内容之一。用导数来判断函数的单调性,其一般步骤为:
(1) 确定函数 的定义域; 的定义域;
(2) 求导函数 ; ;
(3) 在函数 的定义域的范围内解不等式 的定义域的范围内解不等式 或 或 ; ;
(4) 根据(3)的结果确定函数 的单调区间。 的单调区间。
例1:求函数 的单调区间 的单调区间
解:函数 的定义域为 的定义域为 , ,
解不等式 ,得 ,得 ;解不等式 ;解不等式 ,得 ,得 或 或
所以 的单调递减区间为 的单调递减区间为 ,单调递增区间为 ,单调递增区间为 。 当我们遇到含参数函数时,基本上也要按照这个步骤进行。 。 当我们遇到含参数函数时,基本上也要按照这个步骤进行。
例2:求函数 的单调减区间 的单调减区间
解:函数 的定义域为 的定义域为 , ,
解方程 ,得 ,得 , ,
只需解不等式 即可,但需要对 即可,但需要对 之间的大小关系进行讨论。 之间的大小关系进行讨论。
若 ,即 ,即 时, 时, 的解集为: 的解集为:
若 ,即 ,即 时, 时, 的解集为: 的解集为:
所以,当 时, 时, 的单调递减区间为 的单调递减区间为 ; 当 ; 当 时, 时, 的单调递减区间为 的单调递减区间为
通过例2可以发现,含参数函数问题,往往需要分类讨论,而且有的时候,含参数类
问题的讨论并不仅仅像例2那样,只是对两个根之间大小关系的讨论二次函数,其讨论的过程会更加
复杂,运算会更加繁琐。不少同学解答起来会感觉很混乱,无从下手。下面,就对上述问题
进行一些探讨和研究中国学术期刊网。看看如何才能在这个混乱的“局面”中找到解题的思路,做到“乱中
有序”。
先看一个例题:
例3:设函数 ,其中 ,其中 ,求 ,求 的单调区间。 的单调区间。
分析:函数 的定义域为 的定义域为 , ,
这里通过通分的方法,得到 ,这样做的好处是显而易见的,因为 ,这样做的好处是显而易见的,因为
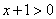 ,所以只需判断好 ,所以只需判断好 的符号。不妨设 的符号。不妨设 , ,
则 ,不等式 ,不等式 等价于 等价于 ,不等式 ,不等式 等价于 等价于 , ,
看来问题可以得到解决了,但是在解决的过程中,有一些确是不容回避的:
(1)  是否为二次函数?这需要通过对 是否为二次函数?这需要通过对 或 或 来加以讨论; 来加以讨论;
(2) 若 为二次函数,则 为二次函数,则 是否恒为正(负)?这一点,可以通过判别式 是否恒为正(负)?这一点,可以通过判别式 来判断。 来判断。
(3) 若 ,则方程 ,则方程 的两个解 的两个解 之间的大小关系是否确定? 之间的大小关系是否确定? 是否在定义域 是否在定义域 内?如不确定需要分类讨论,这也直接关系到不等式 内?如不确定需要分类讨论,这也直接关系到不等式 或 或 的解集。 的解集。
1/3 1 2 3 下一页 尾页 |


