 (3-3)
 (3-4)
戴祖祥（1997）认为由于进出口需求量不能够直接观察到，故无法直接进行回归分析，因此假定进出口需求与进出口量之间服从存量调整假说，即需求量和存量之间满足如下关系：
 (3-5)
 (3-6)
其中， 、 分别表示出口量和进口量，把(3-5)式和(3-6)式分别代入(3-3)式和(3-4)式得：
 (3-7)
 (3-8)
由于美国和日本在华FDI与美中贸易总体上存在互补关系，即美日在华FDI将会推动美中贸易（无论进口还是出口）的增长（何菊香,2009）。鉴于此，引入美日对华FDI,于是由(3-7)和(3-8)确定的方程为：
(3-9)
(3-10)
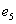其中， 和 表示进口、出口需求的价格弹性， 和 分别表示进口、出口需求的收入弹性， 、 分表示进口、出口数量对日本向华外商直接投资变动的短期弹性， 、 分表示进口、出口数量对美国向华外商直接投资变动的短期弹性。
3.中国对美国出口的贸易弹性分析
（1）指标选择和数据说明
中国向美国出口的数量X：在计算此项指标时，作者借鉴孙文莉（2009）的做法，采用公式：
中国向美国出口数量=中国向美国出口额/中国出口价格
其中，中国向美国出口额月度数据来源于中国商务部和海关总署网站，由于该数据是以现价计算的，也没有进行季节调整，故需要进行定基（采用CPI调整）和季节调整处理；中国没有公布出口价格的数据，故采用中国零售物价指数（RPI）月度数据来代替，但需要做汇率调整，调整公式为：中国出口价格=中国零售物价指数/当期名义汇率，名义汇率数据来源于中国人民银行网站，RPI数据来源于中经网统计数据库和凤凰网。
中国出口相对价格P：在计算此项指标时，采用公式：
中国出口相对价格=中国出口价格/美国物价指数
其中，美国物价指数采用美国消费者物价指数（CPI）,CPI数据来源于国际劳工组织劳动统计数据库。
美国实际收入Y：由于美国没有公布月度GDP数据，故采用每个季度GDP的均分来代替，实际季度GDP采用经季节调整的折年率。
美国对华实际投资额FDI：数据来源于商务部和高校财经数据库。由于商务部没有公布2009年7月美国对华投资额，故采用2009年1-8月投资额减去1-6月投资额，其差值均分为7、8月的实际投资额。
日本对华实际投资额FDI：数据来源于商务部高校财经数据库。由于商务部没有公布2009年7月美国对华投资额，故采用2009年1-8月投资额减去1-6月投资额，其差值均分为7、8月的实际投资额。
上述所有指标都采用2005.7-2009.12月的月度数据，均调整成以2005年7月为基期，各变量的时间序列数据均使用X-12方法进行季节调整。为了使各系列趋势线性化，消除异方差性，并易于分析弹性，对各个序列取自然对数。经季节调整和定基处理后的数据见附录。本文的季节调整和模型估计及检验均使用Eviews5.0软件完成。
（2）实证分析
时间序列平稳性检验
以时间序列数据为依据的实证分析都假定序列是平稳的，否则就会出现伪回归的错误。本文采用ADF检验（AugmentedDickey-Fullertest），考察时间序列变量是否平稳，结果如表3.1.
表3.1各变量的单位根检验结果
|
变量名称
|
检验形式（C，T，L）
|
ADF统计量
|
1%临界值
|
5%临界值
|
10%临界值
|
|
lnX
|
（C，0，1）
|
-1.213281
|
-3.562669
|
-2.918778
|
-2.597285
|
|
dlnX
|
（C，0，0）
|
-11.82418
|
-3.562669
|
-2.918778
|
-2.597285
|
|
LnP
|
（C，T，1）
|
-1.690045
|
-4.144584
|
-3.498692
|
-3.178578
|
|
dLnP
|
（C，0，0）
|
-4.420406
|
-3.562669
|
-2.918778
|
-2.597285
|
|
lnY
|
（C，0，3）
|
-2.407650
|
-3.568308
|
-2.921175
|
-2.598551
|
|
dlnY
|
（0，0，1）
|
-15.59901
|
-2.612033
|
-1.947520
|
-1.612650
|
|
lnFDI
|
（C，0，1）
|
-0.783737
|
-2.610192
|
-1.947248
|
-1.612797
|
|
dlnFDI
|
（C，0，0）
|
-12.33147
|
-3.562669
|
-2.918778
|
-2.597285
|
|
lnFDI
|
（C，0，0）
|
-3.558089
|
-3.560019
|
-2.917650
|
-2.596689
|
|
dlnFDI
|
（C，0，0）
|
-9.846089
|
-3.562669
|
-2.918778
|
-2.597285
|
说明：表中的检验类型（C，T，L），C和T表示带有常数项和趋势项，L表示所采用的滞后阶数，根据AIC和SC最小来确定滞后阶数。*表示检验值是显著的，表明检验值在1%的水平下不显著，无标志表明检验值不显著，接受具有单位根的原假设。
从表3.1中的检验结果可以看出，中美出口弹性的所有变量在1%的显著水平下都遵循一阶单整。
格兰杰因果检验
由单位根检验可知中美出口弹性的各个变量的一阶差分是平稳的，可以做格兰杰因果关系检验，据AIC确定的各变量的滞后阶数为3。各变量因果关系检验见表3.2。
表3.2格兰杰因果关系检验结果
|
零假设
|
F统计值
|
概率
|
|
lnP1不是lnX的格兰杰原因
|
3.22336
|
0.03152
|
|
lnX不是lnP1的格兰杰原因
|
0.71220
|
0.54995
|
|
lnY1不是lnX的格兰杰原因
|
3.75834
|
0.01734
|
|
lnX不是lnY1的格兰杰原因
|
0.68274
|
0.56735
|
|
lnFDI不是lnX的格兰杰原因
|
3.81989
|
0.01620
|
|
lnX不是lnFDI的格兰杰原因
|
1.05027
|
0.37988
|
|
lnFDI1不是lnX的格兰杰原因
|
5.34291
|
0.00316
|
|
lnX不是lnFDI1的格兰杰原因
|
0.85753
|
0.47022
|
由表3.2可知，lnX不是lnP、lnY、lnFDI、lnFDI的格兰杰原因，但它们都是lnX的格兰杰原因。
回归分析
仅用格兰杰检验还不能充分判断变量之间的具体关系，还必须进行OLS估计，估计结果如表3.3所示。
表3.3中国对美国出口的贸易弹性分析
|
R ：0.81873 F：42.45669 DW：2.130194
|
|
LNX = - 40.49969 - 1.378005*LNP + 4.328171*LNY + 0.013532*LNFDI
(-6.060285) (-10.03284) (6.119006) (0.429668)
- 0.034561*LNFDI + 0.271563*AR(1)
(-0.980276) (1.881314)
|
说明：括号里为t统计值，*、**分别表示10%和1%水平下的显著性。
由估计结果可知，中国出口相对价格提高1%，中国对美国出口数量就减少1.38%；美国实际收入增加1%，中国对美国出口数量将会因此上升4.33%，相比之下，美国实际收入对中国出口数量的影响最大。 2/5 首页 上一页 1 2 3 4 5 下一页 尾页 |
