| 1982—1989年的数据来自于睢党臣:《农村公共产品供给结构研究》中的资料,1990—2007年的资料来源于《2008年中国卫生统计年鉴》和各年卫生事业公报。
多元线性回归是指若应变量Y同时受到m个自变数X、X、…、X的影响,且这m个自变数皆与Y成线性关系,则这m+1个变数的关系就形成m元线性回归。因此,一个m元线性回归总体的线性模型为: ,其中, ,其中, ~N(0, ~N(0, )。相应的,一个m元线性回归的样本观察值组成为: )。相应的,一个m元线性回归的样本观察值组成为: 。 。
在多元回归系统中,b一般很难确定其专业意义,它仅是调节回归响应面的一个参数;b(i=1,2,…,m)表示了各个自变数x对y的各自效应,而 则是这些各自效应的集合,代表着所有自变数对应变量的综合效应。 则是这些各自效应的集合,代表着所有自变数对应变量的综合效应。
在建立多元线性回归模型中,以农业总产值为应变量Y,农村基本建设投资为X1,农村教育投入为X2,农村医疗卫生投入为X3,科技三项费为X4,并均取对数,建立双对数线性回归模型。
(二)实证模型分析
分析农业综合生产能力和农村公共产品之间的关系,对各变量取对数,建立以下多元线性回归模型:

根据我们已有的知识,农业产出和教育、科技、医疗、基础建设投资等方面存在相互促进的关系,为使估计结果准确,我们首先检验是否存在多重共线性
1.辅助回归判定系数检验是否多重共线
利用Eviews5.0软件,将模型中的每个解释变量分别对其余解释变量进行回归,以检验是否存在多重共线性,结果如下:
LNX1=1.2967LNX2+0.1498LNX3-0.1049LNX4-1.5474 =0.9873 =0.9873
LNX2=0.4202LNX1+0.2724LNX3+0.1267LNX4+1.1245 =0.9919 =0.9919
LNX3=0.1626LNX1+0.9128LNX2+0.0171LNX4-0.2788 =0.9801 =0.9801
LNX4=-0.2939LNX1+1.0951LNX2+0.0440LNX3-3.3143 =0.8870 =0.8870
从上面结果中可以看出,四个变量之间存在严重的多重共线性。
2.运用Frisch综合分析法消除多重共线
Frisch综合分析法也称逐步回归法,由于此法剔除了不显著的变量,因此无需求解一个很大阶数的回归方程,提高了计算效率;又由于忽略了不显著的变量,避免了回归方程中出现系数很小的变量而导致的回归方程计算时出现病态,得不到正确的解。采用逐步回归法选取显著变量以建立“最优”回归方程,基本步骤是首先把被解释变量对每一个解释变量分别进行回归,从而得到所有的基本回归方程式,并对每一个基本回归方程进行统计检验,分析其估计结果,从中选择最合适的基本回归方程,然后再逐一增加其他解释变量,重新再作回归。
(1)建立应变量与各个自变量的一元回归模型,找出基本方程。
运用最小二乘法逐一求LNY对各个变量的回归。
LNY=0.5413LNX1+5.0226 =0.9731 =0.9731 =0.9720 =0.9720
LNY=0.7588LNX2+4.2760 =0.9740 =0.9740 =0.9729 =0.9729
LNY=0.6561LNX3+4.6521 =0.9858 =0.9858 =0.9852 =0.9852
LNY=0.8962LNX4+7.5134 =0.8345 =0.8345 =0.8276 =0.8276
据上得出,农村卫生医疗投入的拟合优度最高,所以将 作为最基本的模型。 作为最基本的模型。
(2)将其余变量逐个引入模型,估计结果列入表1,2(括号内的数为t统计量值)
表1逐步回归分析结果(一)
|
模型
|
LNX1
|
LNX2
|
LNX3
|
LNX4
|

|

|
|
LNY=f(LNX3)
|
|
|
0.6561
(40.8049)
|
|
0.9852
|
0.9858
|
|
LNY=F(LNX3,LNX2)
|
|
0.1588
(1.2237)
|
0.5210
(4.6726)
|
|
0.9855
|
0.9867
|
|
LNY=f(LNX3,LNX1)
|
0.1508
(2.0245)
|
|
0.4771
(5.3180)
|
|
0.9869
|
0.9879
|
|
LNY=f(LNX3,LNX4)
|
|
|
0.7024
(16.1273)
|
-0.0739
(-1.1425)
|
0.9854
|
0.9866
|
从表1中可以看出,在基本模型中引入LNX2之后,虽然拟合优度 有所增加,但是t检验不显著;引入LNX1,t检验显著,而且 有所增加,但是t检验不显著;引入LNX1,t检验显著,而且 有了很大的提高;引入变量LNX4后, 有了很大的提高;引入变量LNX4后, 有了一点点提高,但是系数的符号不合理,t统计量的检验也不够显著。所以相对来说,模型LNY=f(LNX3,LNX1)的拟合优度最高,所以再将该模型作为基本模型,逐步引入其他变量。 有了一点点提高,但是系数的符号不合理,t统计量的检验也不够显著。所以相对来说,模型LNY=f(LNX3,LNX1)的拟合优度最高,所以再将该模型作为基本模型,逐步引入其他变量。
表2显示,引入LNX2后,拟合优度下降,而且变量的符号也不符合实际;引入LNX4后,拟合优度上升,但是t检验量不显著;将全部变量引入,导致LNX1、LNX2和LNX4的t检验量均不显著。
表2逐步回归分析结果(二)
|
模型
|
LNX1
|
LNX2
|
LNX3
|
LNX4
|

|

|
|
LNY=f(LNX3,LNX1,LNX2)
|
0.1752
(1.5597)
|
-0.0549
(-0.2950)
|
0.4948
(4.5190)
|
|
0.9863
|
0.9880
|
|
LNY=f(LNX3,LNX1,LNX4)
|
0.1693
(2.3190)
|
|
0.5152
(5.7221)
|
-0.0960
(-1.5986)
|
0.9877
|
0.9892
|
|
LNY=f(LNX3,LNX1
LNX4,LNX2)
|
0.1449
(1.3103)
|
0.0583
(0.3001)
|
0.4993
(4.7064)
|
-0.1033
(-1.5643)
|
0.9872
|
0.9892
|
经过以上的逐步引入检验过程,最终确定农业生产总值的函数应该为:
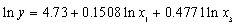 (1) (1)
t:(2.0245)(5.3180)
 =0.9879 =0.9879 =0.9869D.W.=0.7301 =0.9869D.W.=0.7301
3.利用Eviews显示拟合效果图如下:
图一回归拟合曲线图
4.进一步建模检验
模型(1)中,D.W.值太小,而且根据上面的回归拟合曲线图,残差 呈现有规律地变动,自相关检验也显示,偏相关系数PAC在1-2期分别>0.5,所以该模型存在一阶和二阶自相关性。 呈现有规律地变动,自相关检验也显示,偏相关系数PAC在1-2期分别>0.5,所以该模型存在一阶和二阶自相关性。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |


