摘要:基于模糊C均值聚类的图像分割法是图像分割领域中广泛应用的一种算法,特别适合解决灰度图像中存在的模糊和不确定性的问题。但是由于噪声等干扰因素的影响,使得利用传统的聚类方法进行图像分割得不到满意的结果,鉴于此,本文提出了基于二维直方图加权的塔形模糊c均值聚类算法和基于统计检验指导的WFCM算法。
论文关键词:图像分割,聚类分析,FCM,WFCM,塔形分解
图像分割是数字图像处理中的关键技术之一,图像分割的好坏直接影响对计算机视觉中的图像理解。在众多的图像分割算法中,基于聚类分析的图像分割方法是图像分割领域中一类极其重要和应用相当广泛的算法。传统的聚类分析是一种硬划分,它把每个待辨识的对象严格地划分到某个类中,具有非此即彼的性质,因此这种分类的类别界限是分明的。而实际上大多数对象并没有严格的属性,它们在性态和类属方面存在着中介性,适合进行软划分。Zadeh提出的模糊集理论为这种软划分提供了有力的分析工具,人们开始用模糊的方法来处理聚类问题,并称之为模糊聚类分析,将模糊聚类分析引入图像分割之中,便形成了模糊聚类图像分割技术。
基于模糊C均值聚类的图像分割方法是图像分割领域中广泛应用的算法。FCM算法的本质上是一种局部搜索寻优技术,它是通过极小化目标函数来求得最优解。基于模糊C均值聚类的图像分割方法适合解决灰度图像中存在的模糊和不确定性的问题。但是,在实际的图像中,由于噪声等干扰因素的影响,使得利用传统的聚类方法进行图像分割得不到满意的结果。鉴于此,本文提出了一种基于二维直方图加权的塔形模糊c均值聚类算法。
二、加权FCM算法
模糊C均值聚类算法(FCM),是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。它早期作为硬均值聚类(HCM)算法的一种改进,在1973年,由Bezdek提出。
FCM算法可如下描述:
初始化:给定聚类别数c,2≤c≤n,n是数据个数,设定迭代停止阈值 ,初始化聚类中心 ,初始化聚类中心 ,设置迭代计数器b=0。 ,设置迭代计数器b=0。
步骤1:用式(1.1)计算或更新划分矩阵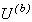 。 。
对于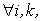 如果 如果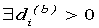 ,则有 ,则有
 (1.1) (1.1)
如果 ,使得 ,使得 ,则有 ,则有
 ,且对j≠r, ,且对j≠r, (1.2) (1.2)
步骤2:用式(1.3)更新聚类原型模式矩阵 。 。
 (1.3) (1.3)
步骤3:如果 ,则算法停止并输出划分矩阵U和聚类原型P,否则令b=b+1,转向步骤1。其中 ,则算法停止并输出划分矩阵U和聚类原型P,否则令b=b+1,转向步骤1。其中 为某种合适的矩阵范数。 为某种合适的矩阵范数。
由于FCM算法也存在不足之处,它不考虑不同样本矢量对聚类效果的不同影响,为此我们提出了基于样本加权的FCM算法,简称WFCM算法。
假设 为p维实数空间中给定的一个有限样本子集,对于任意给定的类别数c,2≤c≤n,样本集X的加权模糊c均值(WFCM)聚类问题可以表示成如下的数学规划问题: 为p维实数空间中给定的一个有限样本子集,对于任意给定的类别数c,2≤c≤n,样本集X的加权模糊c均值(WFCM)聚类问题可以表示成如下的数学规划问题:
 (1.4) (1.4)
其中, 为每个样本的加权系数,且满足概率约束条件 为每个样本的加权系数,且满足概率约束条件 ; ; 为模糊划分矩阵。 为模糊划分矩阵。
利用拉格朗日乘子法,可以推导出式(1.4)的优化迭代公式:
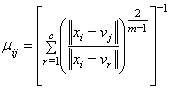 (1.5) (1.5)
 (1.6) (1.6)
三、基于统计检验指导的WFCM算法
在复杂背景下的多目标情况下,往往需要多阈值分割。因此如何选择合适的阈值数目,就成为WFCM图像分割算法的瓶颈。基于WFCM的图像分割算法中假定背景和目标在一维或二维直方图中对应不同的波峰。WFCM算法进行图像分割就对应着直方图中峰态的分解,当分解得到的每个聚类均为单峰分布时,表明峰态分解完全。此时得到的聚类数目最合适。反之就需要继续分解。另外,如果所得到的图像的直方图为单峰分布,就说明基于直方图无法实现图像的分割。这时就无需用WFCM进行图像分割。为此,提出了基于统计检验指导的多阈值图像分割方法。
基于统计检验指导的多阈值图像分割方法步骤为:
步骤1:统计得到图像的一维或二维直方图。
步骤2:对直方图进行单峰分布的统计检验。
步骤3:如果待分析的图像的直方图检验出为单峰分布,则图退出图像分割。
步骤4:如果待分析的图像的直方图检验出为多峰分布,则令聚类数目C为2,然后用基于直方图的WFCM算法对图像进行聚类,对得到的C个类别分别进行单峰检验,只要还有一个子集不满足 显著性经验,就说明还存在可分性。 显著性经验,就说明还存在可分性。
步骤5:令C=C+1重新聚类,直到所有C个子集都不具有可分性后,说明每个类都是单峰分布了,就能输出令人满意的阈值数目和理想的图像分割结果了。
四、基于二维直方图的塔形加权FCM图像分割算法
基于二维直方图的塔形加权FCM图像分割算法将样本集设为广义图像的二元组灰度值,加权系数是各二元组出现的频度。这种算法在执行时,以二维直方图作为带聚类的样本集,利用塔形分解构造出两层的金字塔,即塔顶和塔底。首先在塔顶执行WFCM算法,希望快速地、较为准确地寻找到一个比较合适的聚类中心。然后将其映射至原始待聚类的大数据量的样本空间,即塔底中,再次利用WFCM算法,获得样本集的模糊划分,最终获得图像分割的结果。
根据上述分析,我们可以将基于二维直方图的塔形加权FCM图像分割算法描述如下:
步骤1:输入原始图像,然后用基于高阶统计量的图像平滑去噪方法获得它的平滑图像。
步骤2:利用塔形分解来构造二维直方图,获得塔顶和塔底。
步骤3:初始化塔顶层的聚类类别数才c,m=2,对于塔顶层聚类中心,利用公式(1.7)初始化在二维直方图底面的对角线上;设定每一层迭代停止阈值 。 。
 (1.7) (1.7)
其中L=128,i=1,2,…,c
步骤4:利用加权模糊C均值聚类算法对塔顶层进行模糊聚类。
步骤5:如果相邻两次迭代中顶层的隶属度U矩阵相减后的最大值小于 ,则算法停止并输出聚类中心矩阵P,否则转向步骤4。 ,则算法停止并输出聚类中心矩阵P,否则转向步骤4。
步骤6:用塔顶层输出的聚类中心P合理地初始化塔底层的聚类中心。
步骤7:利用加权模糊C均值聚类算法对塔底层进行模糊聚类。
1/2 1 2 下一页 尾页 |


