论文导读::本文从违约概率衡量上市公司信用风险的角度和信用评级的角度来看,基于因子分析的Logistic回归模型和KMV模型都能反映上市公司的信用风险状况,但基于因子分析的Logistic回归模型的评级结果比KMV模型较准确。
论文关键词:信用风险,KMV模型,Logistic回归模型,因子分析,信用评级
一、引 言
随着金融全球化趋势的加快和金融市场的波动性加剧,企业破产和重组事件的发生频率也越来越高,各国金融行业受到了前所未有的信用风险的挑战。而上市公司是中国证券市场的基础,公司质量的高低、行为的规范与否及其财务状况的好坏将直接影响到中国证券市场的发展和投资者的利益,影响市场的兴衰。
二、数据来源
本文选取上市公司中的绩差股与绩优股为研究样本,绩差股选取截止2005年12月31日沪深两市被ST的上市公司中的30家为样本和绩优股选取大盘蓝筹股中的30家上市公司作为配对样本,共60家上市公司,这60家上市公司全部为A股(研究的股票交易数据和年报财务数据以及相关的其他信息来自大智慧和中国金融wind数据库)。
三、模型的构建及结论分析
针对Logistic回归模型和KMV模型存在的问题,在本文中也做了部分的改进,进而对中国上市公司进行信用风险度量,以期待能找到适合中国实际情况的信用风险度量模型。
3.1、Logistic回归模型
对Logistic回归模型的构建,首先要慎重选择参数。误选参数会导致模型的误判。
3.1.1 、Logistic回归模型的参数选择
本文选择了能反映上市公司的赢利性,偿债能力,营运能力、现金流量等方面特性的21个财务指标。我们利用SPSS13.0统计软件作为因子分析的工具金融论文,其具体步骤如下:
(1)提取60家样本公司2005会计年度报告的指标数据,利用SPSS13.0现将21个指标进行无量纲标准化;
(2)利用因子分析计算相关系数矩阵的KMO值及Barlett检验值,分析显示KMO值及Barlett检验值符合检验要求;
(3)计算特征值、贡献率、共同度,提取特征值大于0.8的9个因子为主要因子,累计贡献率达到81.687%[2]。其中第一个主因子的方差贡献率为26.992%,第二个主因子的方差贡献率为14.646%,第三个主因子的方差贡献率为8.298%,后边的几个主因子的贡献率依次降低。
(4)建立因子载荷矩阵、因子得分系数矩阵,求得9个主因子的因子得分。
在运用SPSS13.0对财务指标进行因子分析时,我们采用的是主成分分析方法,求旋转后的因子载荷矩阵选择最大方差旋转法。结果分析如下:
(a)KMO和球形Bartlett检验
经KMO和Bartlett检验表明:Bartlett球度检验的值为838.034,概率 ,即假设被拒绝,也就是说,可以认为相关系数矩阵与单位矩阵有显著差异。同时KMO值为0.636,根据KMO度量标准[3]可知,原变量适合进行因子分析。 ,即假设被拒绝,也就是说,可以认为相关系数矩阵与单位矩阵有显著差异。同时KMO值为0.636,根据KMO度量标准[3]可知,原变量适合进行因子分析。
(b)因子分析的总方差解释
因子分析总方差列表中显示前9个主成分的特征值大于0.8,但他们的累积贡献率达到了81.687%,在特征根大于1的情况下,有7个主要因子,他们的累积贡献率达到了73.64%,模型的解释力度相对较低。并由各个成分特征值的碎石图可知,保留前7个主要因子就可以概括绝大部分的信息,但这7个累积贡献率低于80%。
(c)因子分析的共同度
从因子分析的共同度表中的第二列显示初始共同度,全部为1;第三列是提取特征根的共同度,本文中是在指定特征根大于0.8的条件下的共同度,可以看到,总资产同比增长率和销售净利率的共同度较低(低于80%)金融论文,这几个变量的信息丢失较为严重。 但大部分的共同度都在0.7以上,且大部分大于0.8,说明这9个公因子能够较好地反映原各指标变量的大部分信息。
3.1.2、Logistic回归模型的构建
我们把这9个主因子都引入到Logistic回归模型中,进行多元回归分析。利用SPSS13.0统计分析软件的BinaryLogistic回归程序包进行回归,得到的结果如表4-7,4-8所示论文格式范文。
从回归的第一步Cox & Snell 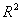 为0.639,Nagelkerke 为0.639,Nagelkerke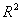 为0.851,大于0.8,说明该模型的拟合效果较好[4]。从表4-7可以得到,模型的整体准确判别率为93.3%,模型对上市公司的违约判别率还是较好的。从表4-8可以看出,9个主因子的显著性水平都较高,第9个主因子的显著性最大,为0.755,相对来说第2、4及5个主因子显著性水平较低。 为0.851,大于0.8,说明该模型的拟合效果较好[4]。从表4-7可以得到,模型的整体准确判别率为93.3%,模型对上市公司的违约判别率还是较好的。从表4-8可以看出,9个主因子的显著性水平都较高,第9个主因子的显著性最大,为0.755,相对来说第2、4及5个主因子显著性水平较低。
表4-7 输出结果

表4-8 模型的回归系数
Variablesin the Equation
|
|
B
|
S.E.
|
Wald
|
df
|
Sig.
|
Exp(B)
|
|
Step 1(a)
|
FAC1_1
|
.934
|
1.133
|
.679
|
1
|
.410
|
2.544
|
| FAC2_1 |
3.143
|
1.270
|
6.130
|
1
|
.013
|
23.180
|
| FAC3_1 |
2.648
|
1.498
|
3.124
|
1
|
.077
|
14.126
|
| FAC4_1 |
5.401
|
2.207
|
5.990
|
1
|
.014
|
221.581
|
| FAC5_1 |
6.244
|
2.681
|
5.422
|
1
|
.020
|
514.663
|
| FAC6_1 |
-.491
|
.615
|
.636
|
1
|
.425
|
.612
|
| FAC7_1 |
1.775
|
1.065
|
2.777
|
1
|
.096
|
5.900
|
| FAC8_1 |
.686
|
1.574
|
.190
|
1
|
.663
|
1.987
|
| FAC9_1 |
.872
|
2.795
|
.097
|
1
|
.755
|
2.393
|
| Constant |
.480
|
1.185
|
.164
|
1
|
.686
|
1.615
|
将这9个主因子全部纳入模型,得到Logistic回归方程如下:
 即 即
上式就是所要构造的Logistic回归模型。
3.1.3、Logistic回归模型的结果分析
在用SPSS13.0统计软件在做Logistic回归时,取系统默认的 为分界点。假定当 为分界点。假定当 时,将其视为违约公司, 时,将其视为违约公司, 则将其成为非违约公司。 则将其成为非违约公司。
对于违约组的30家上市公司,判为违约的有29家,非违约的有1家,即ST盐湖,违约概率为0.484850,误判率为3.3%。绩优股的30家上市公司中,有3家被误判为违约股,分别为:ST金杯、ST天桥和锌业股份,违约概率分别为:0.961318、0.854739、0.581011,误判率为10%。因此金融论文,Logistic回归模型对于ST公司和非ST公司的判别准确率为:96.7%、90%。
3.2、 KMV违约模型
KMV模型的基本假设是:当公司的资产价值低于一定水平时,公司就会对债权人和股东违约。
3.2.1 参数的假定
在KMV模型中,有三个关键性的指标即资产价值 、资产价值波动率 、资产价值波动率 及公司债务合同上的债务数量。 及公司债务合同上的债务数量。
(1)股权价值
因为本文选取的是2005年的上市公司,不存在非流通的上市流通。本文选择用每股净资产代替非流通价格来计算股权价值。从而得到股权价值的计算公式为:
股权价值=流通股股数×市价+非流通股股数×每股净资产
(2)股权价值的波动率
在Block-Scholes期权定价模型中,变量 指股票收益率波动性,即标准差。企业违约与否,主要看企业资产价值变化率的标准差。本文以上市公司股票的波动率代替股权价值的波动率。采用历史波动率法估计上市公司股权市场价值未来一年的波动率。假定股票价格S满足对数正态分布。股票收益的日波动率为: 指股票收益率波动性,即标准差。企业违约与否,主要看企业资产价值变化率的标准差。本文以上市公司股票的波动率代替股权价值的波动率。采用历史波动率法估计上市公司股权市场价值未来一年的波动率。假定股票价格S满足对数正态分布。股票收益的日波动率为:

其中, , , 为股票每日相对收益率, 为股票每日相对收益率, 为 为 的均值。 的均值。
假定年交易天数为250天,则年波动率为:

(3)违约点的选择
本文借鉴翟东升等(2007)[27]的研究成果。设STD为短期负债,LTD为长期负债,选取的违约点为:
DP=STD+0.75LTD
(4)债务有效期限
为了计算的方便,在本文中,取债务的有效期限为1年。
(5)无风险利率
我们用银行2005年一年期定期存款的基准利率来代替无风险利率,即r=2.25%。数据来自中国人民银行网站。最后,我们假定未来公司资产价值的增长率为零。
3.2.2 KMV模型的实证结果分析
我们利用mathcad软件来两个方程进行求解,求出资产价值 和资产价值波动率 和资产价值波动率 。进而可以求出上市公司的违约距离。我们将ST上市公司和非ST上市公司的DD分为3个区间: 。进而可以求出上市公司的违约距离。我们将ST上市公司和非ST上市公司的DD分为3个区间: , , , , ,并在这3个区间上公司出现的频数和频率,如表4-12所示: ,并在这3个区间上公司出现的频数和频率,如表4-12所示:
表4-12 30家ST上市公司和30家非ST上市公司的违约距离统计
1/2 1 2 下一页 尾页 |


