论文导读::本文基于2010年中国加大对房地产行业调控的现状和中国房地产上市公司独有的特点,运用修正后的KMV模型,选取沪深两市27家房地产上市公司的数据进行实证研究,根据实证结果,判别修正后的KMV模型适用性并分析违约距离的合理控制范围。
论文关键词:KMV模型,信用风险,违约距离
1.引言
2010年来,国家针对房地产的政策不断出台,致使房地产公司发展面临诸多风险。 2010年11月份,银监会抽取60家大型房地产公司调研的结果表明:负债率整体上升,资金链趋紧金融论文,信用风险已成为房地产公司监管层心头之患。本文采用修正的KMV模型,以求更适合我国房地产上司公司的特点,更加有效的对数据进行实证研究,分析公司在信用风险管理中应将违约距离控制在哪一个范围cssci期刊目录。
2.KMV模型的基本原理
KMV模型是根据Merton将有关期权定价理论运用于风险贷款和证券投资而开发出的一种实用高效的分析模型,用以衡量公司的信用风险。
KMV模型又称预期违约率模型(expected default frequency,EDF模型),该模型将企业负债看作是买入一份欧式看涨期权,即企业所有者持有一份以公司债务面值为执行价格,以公司资产市场价值为标的欧式看涨期权。如果负债到期时企业资产市场价值V高于其债务D,公司偿还债务,企业股东权益的价值为偿还债务后的剩余金融论文,即V-D;而当企业资产市场价值小于其债务时,企业则无法偿还贷款,选择违约,股东权益变得毫无价值,股权所有者将会选择放弃公司的所有权。
KMV模型评价公司信用风险的基本思路是以违约距离DD表示公司资产市场价值期望值距离违约点D (Default Point)的远近,距离越远,公司发生违约的可能性越小,反之越大。违约点D通常处于流动负债与总负债面值之间的某一点;违约距离常以资产市场价值标准差的倍数表示。该模型基于公司违约数据库,根据公司的违约距离确定公司的预期违约概率cssci期刊目录。
3.KMV模型的计算方法
KMV模型的计算有两个重要的步骤:一是利用B-S模型倒推出公司资产的市场价值V及其波动率SV;二是计算公司的违约距离DD并得出一个期望违约率EDF。
3.1 计算公司资产价值V和资产波动率SV
由于公司股权市场价值可以采用B-S期权定价模型来构建公司资产价值和股权价值之间的关系,即:
 (1) (1)
B-S期权定价模型中公司股票的波动率SE和资产的波动率SV之间存在如下关系:  , , 金融论文, 联立得: 金融论文, 联立得:
 (2) (2)
其中,E为公司股权市场价值,V为公司资产价值,N( )为标准正态累积分布函数,  ,D为公司违约点,r为无风险利率,t表示当前时间,信用风险评价通常以一年为时段,设定违约距离的计算时间为一年,即T=1。 ,D为公司违约点,r为无风险利率,t表示当前时间,信用风险评价通常以一年为时段,设定违约距离的计算时间为一年,即T=1。
E、D和SE可以从资本市场上获得,但公司资产价值V以及公司资产的波动率SV这两个变量未知金融论文,于是通过(1)和(2)两个方程组联立用MATLAB软件求解,算出这两个未知数。
3.2计算违约距离DD和期望违约率EDF
违约点D即公司资产价值与公司负债价值相等时的价值,也就是当公司资产价值低于此违约点时,公司就会被视为违约。违约距离DD是指以公司资产价值在风险期限内由当前水平降至违约点的相对距离。假设公司资产价值属于对数正态分布,计算公式为:
 (3) (3)
KMV公司根据违约距离,基于违约数据库,可以映射出公司的期望违约频率EDFcssci期刊目录。由于我国当前还没有公开的违约的数据库可以使用,所以我们暂且采用理论上的预期违约频率来代替。假设公司资产价值服从对数正态分布, 这样就能利用MATHCAD软件计算理论上的违约概率,计算公式为:
 (4) (4)
4.KMV模型的修正
4.1 股权市场价值E的修正
美国上市公司没有非流通股,全部为流通股,而我国上市公司的总股本分为非流通股和通通股,二者同权不同价,所以不能简单地以流通股股价乘以总股本来计算上市公司的股权市场价值。本文对此进行修正,将股权市场价值计算公式确定为:
 (5) (5)
其中,N1为流通股股数金融论文,P1为流通股股价,本文选取每季最后一日收盘价为流通股股价,N2 为非流通股股数,P2 为非流通股股价。
4.2 非流通股股票定价问题的修正
我国的国有股转让主要是协议转让,协议转让价格主要是基于每股净资产的价格上下浮动。本文构造一个线性回归模型,其中自变量为每股净资产指标,因变量为股票实际转让价格,其对应的回归方程如下:
 (6) (6)
其中,P为国有股实际转让价格;X为国有股每股净资产。
本文选取2009年协议转让的50只股票的相关数据利用SPSS.17软件中最小二乘法进行线性回归分析,以确定方程(6)中的参数值及检验方程的可信度,SPSS回归分析结果如表1所示cssci期刊目录。
|
表1 非流通股定价模型回归分析结果
|
|
|
|
未标准化系数
|
Beta
|
t
|
Sig.
|
|
|
|
B
|
标准误差
|
|
方程 1
|
a
|
.495
|
.101
|
|
4.796
|
.000
|
|
b
|
.895
|
.052
|
.946
|
21.930
|
.000
|
因此,回归方程为:
P =0.495 +0.895X(7)
方程的参数t检验以及模型可信度F检验为均在0.05显著水平上通过了检验金融论文,R-squared接近于1,所以本文将方程(7)作为非流通股定价模型,即:
P2 =0.495 +0.895X (8)
5.KMV模型计算
本文运用修正后的KMV模型,选取沪深两市27家2010年前三季度会计信息披露及时全面,真实可靠的房地产上市公司作为样本进行研究。其中,剔除了发行B股和H股的上市公司后,将样本分为三类:第一类样本选取了9家ST房地产上市公司;第二类样本选取的9家非ST公司是资产规模较小而资产负债率较高的公司,这类公司一旦资金链出现问题很容易导致信用违约;第三类样本选择9家房地产行业中的佼佼者,这类公司信用状况和财务状况较好,发生信用风险的概率较低。对27家公司的数据进行实证研究,对其在未来一年的违约距离做出估计金融论文,以此推断违约距离的合理范围。
5.1计算公司股票波动率:
本文采用历史波动率法估计股权市场价值波动率.假设上市公司股票价格满足对数正态分布,则股票周收益率ui为:
 (9) (9)
其中,Si为第i周的股票收盘价,Si/Si-1为股票周相对价格,ui为股票周波动率。
5.2 计算股权市场价值的周波动率标准差Sz和年波动率标准差SE
 (10) (10)
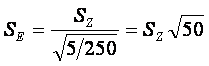 (11) (11)
其中, 是ui的均值,通常一年中的交易日为250天。 是ui的均值,通常一年中的交易日为250天。
5.3计算公司股权市场价值E
5.4 r值的选取
由于计算的需要和我国利率还没有自由化,所以本文假定公司股票价格服从对数正态分布,采用研究期间银行一年期存款利率为无风险利率,即r=2.25%cssci期刊目录。
5.5计算公司违约点D
KMV公司在收集了包括3400家上市公司和40000家非上市公司自1973年以来的资料并且建立了庞大的数据库的基础上,根据大量违约事件的实证分析得出的结论,发现违约发生最频繁的临界点是在公司价值大于等于流动负债(SD)加上的长期负债(LD)的一半,即:
D=SD+0.5LD(11)
其中,SD为流动负债金融论文,LD为长期负债,数据来自各公司2010年资产负债表。
5.6计算公司资产价值V和资产波动率SV
由(1)和(4)组成的方程组共有5个变量,E、D和SE的值本文从国泰君安数据库和巨潮资讯网直接获得或基于直接获得数据利用数学软件间接求得,将已知数据代入方程组,利用matlab7.8迭代技术,计算出V和SV。
5.7计算违约距离DD和期望违约率EDF
得到的数据结果如下表所示:
表2 27家样本公司计算结果
|
一类DD
|
一类EDF
|
二类DD
|
二类EDF
|
三类DD
|
三类EDF
|
|
5.560058
|
1.347E-08
|
1.713010
|
4.300E-02
|
2.380230
|
8.651E-03
|
|
5.455488
|
2.442E-08
|
2.680340
|
3.677E-03
|
1.879287
|
3.000E-02
|
|
4.767909
|
9.307E-07
|
2.132026
|
1.700E-02
|
1.640289
|
5.000E-02
|
|
4.321993
|
7.732E-06
|
2.682521
|
3.653E-03
|
1.758637
|
3.900E-02
|
|
4.051888
|
2.540E-05
|
2.132673
|
1.600E-02
|
2.906977
|
1.825E-03
|
|
3.822208
|
6.613E-05
|
2.955432
|
1.561E-03
|
1.863897
|
3.100E-02
|
|
3.689040
|
1.126E-04
|
1.689571
|
4.600E-02
|
2.064012
|
2.000E-02
|
|
3.535977
|
2.031E-04
|
1.899567
|
2.900E-02
|
1.894128
|
2.900E-02
|
|
3.359638
|
3.902E-04
|
2.113052
|
1.700E-02
|
2.621765
|
4.373E-03
|
表3 样本公司违约距离DD统计特征
|
均值
|
2.112136
|
2.222021
|
4.284911
|
|
最大
|
2.906977
|
2.955432
|
5.560058
|
|
最小
|
1.640289
|
1.689571
|
3.359638
|
|
调和平均数
|
2.043185
|
2.144143
|
4.158532
|
|
中值
|
1.894128
|
2.132673
|
4.051888
|
|
一类与二类均值差
|
0.1098856
|
|
二类与三类均值差
|
2.0628897
|
6.实证分析
6.1实证结果表明:
三类公司的DD值大于二类公司,二类公司的DD值大于一类公司。
一类与二类的DD值相差无几,三类公司与一类、二类的DD值相差甚远。
所以,在中国的股票市场中,运用修正的KMV模型能够识别出房地产上市公司信用风险的差异,具有一定的适用性。
6.2违约距离DD合理控制范围的预测
理论上,本文选取的二类和三类公司均属于信用风险较大的公司,实证研究中DD值再次证明了这一点。所以本文选取其DD值作为变量进行K—均值聚类分析金融论文,将18个DD值分为两类得:
|
|
表4 最终聚类中心
|
|
|
|
|
聚类
|
|
|
|
|
1
|
2
|
|
|
|
DD
|
2.704544
|
1.898346
|
|
|
表5 每个聚类中的案例数
|
|
聚类
|
1
|
6.000
|
|
2
|
12.000
|
|
有效
|
18.000
|
|
缺失
|
.000
|
| |
|
|
|
|
|
|
可见,一类和二类的DD值较凝聚,在聚类分析中都有效,在DD值等于1.898346时是临界点,小于这一值时公司更易发生违约,所以可用违约距离值1.898346来预测房地产上市公司未来会发生违约的依据,但有待更多的实证检验。
参考文献:
[1]冷梅.基于KMV和关联规则的上市公司信用风险传染研究[J].湖南大学学报(社会科学版),2009,(6)
[2]刘博.基于KMV模型对上市公司的信用风险进行度量的实证分析[J].科学技术与工程,2010,(3):843-847
[3]赵煌,毛长飞.KMV模型及其影响因素的实证研究[J].法制与社会,2009,(1):131-132
[4]迟晨.KMV模型对我国上市公司信用风险度量的实证研究[J].海南金融,2010,(2):41-44
|


