| 新课程改革中强调要加强课程内容与学生生活以及现代社会和科技发展的联系,培养学生分析和解决问题的能力数学方法,这就要求师范院校在教学过程中要注意将知识与实际生活多联系,在数学分析教学中利用建模的思想来培养师范生分析、解决问题的能力就是非常有效的一个途径。
2.4转化的思想
将我们要解决的问题通过转化为已经解决或者容易解决的问题上来,从而使问题得到解决的思想就是转化的思想。如海涅定理实现了数列极限与函数极限的转化,格林公式给出了平面上的第二型曲线积分与二重积分之间的转化,无穷小与无穷大、广义积分与级数、重积分与累次积分等都可进行转化。可见,转化是数学分析中常用的一种基本思想。
3.数学方法:
数学中有很多常用的方法,如类比推理法、归纳推广法、猜想发现法等。在解题中,引导学生选取适当的方法解决问题,也是提高学生解题能力的途径之一,同时还可以促使学生多创新,得出更多的结论。
3.1归纳推广
在《数学分析》中,数学概念是比较抽象的,学生往往不明白为什么要这样来定义,有什么用处,所以在讲授数学概念时需要让学生理解问题是怎样提出的,概念是如何形成的。在对相关概念进行讲授时,可通过案例教学,由学生自己归纳得出。例如,对导数这部分内容,不应只停留在要求学生掌握几个求导公式,会进行简单求导上,而应由具有实际背景的实例来引入。导数概念一般是由瞬时速度和切线斜率引入的,当然还可通过研究增长率、膨胀率、效率、密度、加速度、电流强度等反映导数应用的实例来引入,引导学生在实例中归纳出瞬时变化率就是导数。
再如,利用导数讨论函数图象,是大可结合中学实际的。就拿二次三项式的图象的讨论来说,我们知道它的图象是一抛物线,利用导数知识数学方法,从 , , , , 知道当 知道当 时,曲线开口向上,是凸的,而当 时,曲线开口向上,是凸的,而当 时,曲线开口向下,是凹的。当 时,曲线开口向下,是凹的。当 时,即 时,即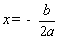 处函数有极值 处函数有极值 。经过这样简单的讨论,利用导数知识,对二次三项式的图象的认识就更清楚了。中学数学中许多极值问题的研究,正是依据二次三项式的知识引出的。而导数的知识给予我们一个更有力的方法,它可以推广到解决更为广泛的极值问题上来。在这部分的教学中,既要注意把应用导数解决极值问题的一般原理教给学生,同时可选取一些中学课本里的极值问题给学生用新的方法去解决,进行比较,让学生体会出用导数求极值的方便之处。 。经过这样简单的讨论,利用导数知识,对二次三项式的图象的认识就更清楚了。中学数学中许多极值问题的研究,正是依据二次三项式的知识引出的。而导数的知识给予我们一个更有力的方法,它可以推广到解决更为广泛的极值问题上来。在这部分的教学中,既要注意把应用导数解决极值问题的一般原理教给学生,同时可选取一些中学课本里的极值问题给学生用新的方法去解决,进行比较,让学生体会出用导数求极值的方便之处。
3.2类比推理
类比推理法是指根据两个问题有一部分特征相类似,从而推出其他特征也可能相类似的一种推理方法。
例如:在讲函数极限的概念时,学生理解起来比较困难,但是,学生对数列极限概念比较熟悉论文服务。教师在讲函数 的极限定义时,可与数列极限定义相类比来启发学生自己给出定义。首先教师指出函数 的极限定义时,可与数列极限定义相类比来启发学生自己给出定义。首先教师指出函数 的极限与数列的极限相类似,都是描述在自变量无限增大的过程中,函数值无限接近于一个常数的变化状态。根据这一特点,可类比数列极限定义来定义函数 的极限与数列的极限相类似,都是描述在自变量无限增大的过程中,函数值无限接近于一个常数的变化状态。根据这一特点,可类比数列极限定义来定义函数 的极限。接着让学生找出数列极限与函数极限的对应关系来: 的极限。接着让学生找出数列极限与函数极限的对应关系来:
|
函数关系式
|

|

|
|
定义域
|
|

|
|
自变量的变化趋势
|

|

|
|
函数值的变化趋势
|

|

|
最后学生根据这个对应关系很容易得出 的定义。这时,教师要向学生说明这种得出定义的方法是类比推理法,在数学分析中有着广泛的应用,如广义积分与定积分、格林公式与高斯公式等的类比数学方法,并向学生介绍类比推理法的内涵及在数学分析中应用这种方法所得出的一些重要结论,让学生充分认识到这种方法的重要性。 的定义。这时,教师要向学生说明这种得出定义的方法是类比推理法,在数学分析中有着广泛的应用,如广义积分与定积分、格林公式与高斯公式等的类比数学方法,并向学生介绍类比推理法的内涵及在数学分析中应用这种方法所得出的一些重要结论,让学生充分认识到这种方法的重要性。
在教学中还要合理运用启发式和发现猜想等方法,注重培养学生的创新思维能力、形象思维能力、发散性思维能力等。如在函数凸性的教学中可以使用直观发现法进行教学,对于莱布尼兹公式,可先让学生观察 , , , , ,学生不难发现,上述几个式子与二项式 ,学生不难发现,上述几个式子与二项式 展开式极为相似,则学生会猜想出 展开式极为相似,则学生会猜想出 , ,
接下来只需用数学归纳法证明这个式子是正确的。对于这个公式的理解,学生通过自己猜想、证明来得出相关结论就要比教师直接证明要有效的多。
培养学生的数学素质,是一项细致而长远的艰巨任务。教师只有努力提高自身数学思想方法的素养,通过数学教学教会学生数学思想方法,才能有效地提高学生的数学素质,以求达到教育的最终目的——为社会输送高素质的实用型的教师。
参考文献:
[1]周焕琴.论师范数学教育中的素质教育[J].安康学院学报.2008.2(1):114.
[2]华东师范大学数学系.数学分析(第三版)[M].高等教育出版社. 2001.
[3]戴振祥.数学分析课程如何联系中学教学的实际[J].徐州教育学院学报.2008.9(3):129.
[4]林远华.数学分析课程中的数学思想方法研究[J].河池师专学报.2001.6(2):31-33.
[5]谭伟明、李连芬、苏芳.数学思想方法与学生数学素养的培养[J]. 梧州学院学报.2009.12(6):70-71.
[6]樊仲光.新升本科院校数学分析教学的几点思考[J].广西教育学院学报.2010(2):139-141.
2/2 首页 上一页 1 2 |


