论文导读::针对师范院校《数学分析》教学现状与适应新课程的教师教育改革,提出当前师范院校数学分析课程应体现的数学思想与方法的渗透与教学,这是实现师范院校培养实用型优秀教师的有效途径。
论文关键词:数学分析,数学思想,数学方法
师范院校承担着为国家培养未来教师的重任,在大力提倡实施素质教育,培养学生创新能力的今天,师范院校的教学应站在培养具有实际应用能力的人才的高度上来改进教学,用现代教学观指导教学。对于数学专业而言,要提高本专业的综合素质,必须培养学生的专业素质即数学素质。数学素质主要是一种数学思维方式,它既包括逻辑思维,也包括从现实生活中提炼数学问题的直觉,形成数学概念的抽象,运用数学语言的能力,构造数学模型的实践以及运用数学知识去解决问题的意识和能力【1】。《数学分析》是师范数学专业最重要的基础课之一,其内容丰富,教学垮时长数学方法,对学生影响深远。《数学分析》不仅是学习某些后续课程的基础,而且在中学数学教学中,如:求切线方程、求极值、判断函数增减性、证明不等式、求弧长等都具有很大的指导作用,它的基本概念、思想和方法可以说无处不在。因此在教学的每一个环节都要注重数学思想方法的渗透。
1、现状:
师范教育历经百年,其教育体制和模式有当时的合理性和历史贡献,但也应看清它的时代局限。
1.1教材内容几乎是纯理论叙述,教师在授课时过分注重理论体系而忽视了应用,与社会实际联系不明显,很难引起学生的兴趣;
1.2教材内容普遍只见定义、定理、推导、证明,而对思想方法则很少提及,教师在数学分析的教学中只重逻辑思维能力和分析运算能力的培养,轻培养学生解决问题的思想方法能力的培养;
1.3教师的教学方法单一,教师教育培养模式大多以封闭模式为主,教育理论和教育实践严重脱节,照本宣科,学生提不起兴趣。
这些缺陷不利于师范生形成宽厚的知识基础、良好的职业技能和优秀的综合素质,制约师范生职后的发展。
2.数学思想
2.1极限的思想
极限思想是数学分析的精髓, 是用来衡量 是用来衡量 和 和 的接近程度的, 的接近程度的, 愈小,表示接近得愈好,它除限于正数外,不受任何限制论文服务。尽管 愈小,表示接近得愈好,它除限于正数外,不受任何限制论文服务。尽管 有它的任意性,但当一经给出,就应暂时看作固定不变的,即 有它的任意性,但当一经给出,就应暂时看作固定不变的,即 又有确定性,给定以后,便可根据它来确定 又有确定性,给定以后,便可根据它来确定 。正是极限概念中扮演主要角色的 。正是极限概念中扮演主要角色的 的二重性,即 的二重性,即 的任意性和确定性数学方法,深刻地反映了有限与无限的对立统一的辩证关系,有机地将有限和无限、初等数学与高等数学结合起来。而数学分析中最重要的一些基本概念几乎都是用极限来定义的,所以极限的正确理解对于学生学好数学分析这门课程有着重要作用。在教学中要紧紧抓住“极限”这条主线,以现实具体的问题为背景(如刘徽割圆术),从具体到抽象,特殊到一般的方法来介绍极限,一方面使学生对“极限”的定义有一个初步的认识,另一方面能让学生了解极限概念的来龙去脉,从而感受极限的思想。 的任意性和确定性数学方法,深刻地反映了有限与无限的对立统一的辩证关系,有机地将有限和无限、初等数学与高等数学结合起来。而数学分析中最重要的一些基本概念几乎都是用极限来定义的,所以极限的正确理解对于学生学好数学分析这门课程有着重要作用。在教学中要紧紧抓住“极限”这条主线,以现实具体的问题为背景(如刘徽割圆术),从具体到抽象,特殊到一般的方法来介绍极限,一方面使学生对“极限”的定义有一个初步的认识,另一方面能让学生了解极限概念的来龙去脉,从而感受极限的思想。
2.2数形结合思想
数形结合的思想,就是充分利用形的直观性和数的规范性,通过数与形的联系转化来研究数学对象和解决数学问题。
例如:设函数 在区间 在区间 上连续,证明: 上连续,证明:
若 是奇函数,则 是奇函数,则
若 是偶函数,则 是偶函数,则
分析:如果按课本那样直接去证明,学生知道了这个等式可用换元法来推导,但是理解起来似乎不那么容易。如果用数形结合的思想方法进行分析,那么结果就很明显了。
   
在图1中, 是奇函数, 是奇函数, 表示由 表示由 , , 及 及 围成图形的面积, 围成图形的面积,
 表示由 表示由 , ,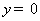 及 及 围成图形的面积, 围成图形的面积,
而 , , ,则 ,则
于是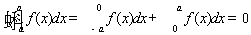
在图2中, 是偶函数, 是偶函数, 表示由 表示由 , , 及 及 围成图形的面积数学方法, 围成图形的面积数学方法,
 表示由 表示由 , , 及 及 围成图形的面积, 围成图形的面积,
而
于是
在数学分析中,还有很多结论可用数形结合的思想来解决,如拉格朗日中值定理、闭区间上连续函数的性质、利用积分区域的图形求重积分等。在教学中可引导学生用数形结合的思想来得出这些结论,这要比纯理论证明更好理解。而在中小学数学中,数形结合思想同样有着广泛的应用。所以对于师范院校,数学分析课程就要注重培养师范生这种数学思想的形成,这对他们今后的教学将会有很大的帮助。
2.3数学建模思想
培养学生的数学素质,数学建模是有效的途径。在信息时代,数学已经不仅仅是一种基础理论,而且还是一种可以直接产生经济效益的数学技术,计算机给数学研究和数学教学带来了深远的影响。因此,在数学分析教学中,充分利用数学建模的思想来进行教学,对培养学生观察力、想象力、逻辑思维能力以及分析、解决实际问题的能力都起到了很好的作用。
例如,在引入无穷级数这一个概念时,可以介绍古希腊哲学家芝诺所提出的“阿基里斯追龟悖论”。芝诺的悖论在于他把阿基里斯追乌龟时,乌龟向前爬的距离分成无限段,然后一段一段加以叙述。芝诺认为阿基里斯永远追不上乌龟,实质就是在无限次追赶中,乌龟向前爬的距离之和为无穷大。在此提出了无限项求和的问题。此前,学生熟知的是有限项求和的概念,如何将有限转为无限呢?很自然地就用到了极限这一概念。利用已知的有限项求和,结合极限方法,得出了无限项求和的基本方法论文服务。这样的设计不但能更好地引进无穷级数的概念,也能极大地激发学生的兴趣。
1/2 1 2 下一页 尾页 |


