| 即变量互换后数据不确定度满足实验的线性回归要求。
此时的线性回归图形窗口则显示如图1。
由程序可知，用于判断线性规划优度的判定系数可利用公式求解,亦可利用Matlab里的互相关系数矩阵函数corrcoef()求解。两者均很简洁。可以看出，此线性回归的判定系数 (r为x和y之间的线性相关系数)很接近于1，故此线性回归的拟合度很好，证明了x和y在此实验中确实存在线性关系，也间接证实了此次实验中β和m可认为是定值，不存在不同时刻β相差很大的问题。同样可知，强迫力矩幅值M和摆轮转动惯量I的比值 亦如此。
故此法利用Matlab编程通过对线性回归方程的拟合，同逐差法一样，可测出阻尼系数。同时利用线性拟合优度判断标准线性相关系数r对线性回归合理性的检验，亦可作为实现 的实时测量的理论基础，却不像逐差法那样作为该理论基础时同样受到 变化限制，尤其是在其不可忽略的情况下。这是本文中的线性回归法除了不存在理论误差和能以较高准确度求出常量和外的另一重要意义。
3.3回归于原理论模型
1)缘由
由3.2可知，利用★★式进行线性回归，由于该方法本身不存在近似理论误差（由下文知由于该方法本身采用线性计算，故而计算机数值计算截断误差亦不存在），其所得出的阻尼系数准确度较高。但在确定最终结果的不确定度时，并不能忽略自变量的不确定度，因为相对于原物理量其数据不确定性经过了放大。这样利用线性回归不确定度计算的理论公式（[2],106-110）,在自变量不确定度也存在且不全相同的情况下,导出的最终测量量的不确定度的结果会很繁琐,且不易于简洁编程实现。而且如前所述，其所采用的自变量与因变量均为合成量亦即间接测量量。具有一定不确定度的最初数据依据相关原理，进行不确定度的传播与合成，导致此时的合成量不确定度会增加，故而其最终结果的精密度不会很高，有必要对其进行进一步研究。
2)利用回归函数nlinfit()和nlparci()
基于以上考虑，需利用最初测量数据进行方法的改进，亦即所采取的方法应尽可能直接利用最初测量数据，以尽可能减小最终结果的不确定性。据此，结合利用Matlab处理实验的实情际况，可以利用其工具箱里所提供的非线性回归功能函数（[3],184-188）来进行最终的处理。这些函数能够在已知非线性模型的情况下，直接利用最初数据求解出所需结果，同时提高准确度与精密度。在此处可用非线性拟合的参数估计函数nlinfit()和给出参数估计值95%的置信区间的函数nlparci()进行,且效果很好。
函数nlinfit()利用经过Levenberg-Marquardt修正的高斯牛顿（Gauss-Newton）算法,亦即梯度-展开算法（[2],224-226）对参数进行最小二乘拟合并使局部得到收敛。由其算法收敛原理可知利用此函数对参数进行求解必须先估计参数的大致范围，并且最终结果会受此影响。经过实际的多次试验亦可得出此结论。
具体到该实验中，为了直接利用所有的最初有用数据以提高精确度，本文所采取的求解阻尼系数的方法理论依据选为未经过任何近似的函数表达式（3.1中的(5)式）。在利用Matlab软件处理的前提下，利用上述功能函数对已知相互函数关系的实验数据进行与理论模型的比较，以确定其中的未知量和。此时必须先估计出原式中的未知量和的大致范围，否则由多次实际试验可知可能出错而不是出现误差。此由上述算法在参数估计区间内局部收敛所导致，并且Matlab里所有非线性优化与拟合函数所基于的数值算法都无法避免此类问题。
由此可看出，按照3.1和3.2中所述方法，能很好的估计出待测量的取值范围，且有较高的准确度，为利用Matlab借助非线性功能函数在待测量范围无法直接预测出的情况下，以高精确度完成该实验提供了一个简洁快速且很准确的途径。
因此，把线性回归估计出的值β=0.0624,m=1.1737作为参数初始值，利用上述函数进行相关编程，得程序运行结果为：
bete=
0.0628
m=
1.1791
ci=
0.06220.0633
1.17141.1867
U=
0.0006
0.0077
sigma=
0.0003
0.0039
R_NL=
0.9905
FR=
1.0000
从编程和运行结果可以看出，由上述函数利用精确的测量量表达式回归，知此时可以用于该实验的判断曲线回归拟合优度的指标(R,FR)值为(0.9905,1.0000)。由于R分辨率与灵敏度很高，且此时很接近于1，故可知此时的拟合效果很好，应采用此时的结果。
所以，由此时的运行结果知，在阻尼档为2的情况下，β=beta=0.0628，m=1.1791，并且这两个测定量所对应的由函数nlparci()所给出参数亦即这两测定量的95%的置信区间分别为[0.06220.0633]和[1.17141.1867]，因此对应于置信水平为95%的扩展不确定分别为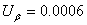 和 。 2/4 首页 上一页 1 2 3 4 下一页 尾页 |
