 , (22) , (22)
式(22)称为渐近段的渐近表达式。在 的零点位置上,公式左端取等号,在其它位置上,公式左端取近似号。由于震荡衰减应力 的零点位置上,公式左端取等号,在其它位置上,公式左端取近似号。由于震荡衰减应力 在趋近端点时趋于消失,所以式(22)的准确性也逐渐提高。 在趋近端点时趋于消失,所以式(22)的准确性也逐渐提高。
转换点也是渐近解显著偏离严格解的起始点,当 大于 大于 ,只有严格解是正确的,界面剪应力的分布只能由严格解确定。自转换点到无穷远,是界面剪应力曲线的基本段。 ,只有严格解是正确的,界面剪应力的分布只能由严格解确定。自转换点到无穷远,是界面剪应力曲线的基本段。
对于界面正应力,有相似的结果,即
(23)
, (24)
5 渐近段界面剪应力奇异分布的特点
基本段内的界面剪应力是由严格解确定的,而渐近段内的界面剪应力虽然也是由严格解确定的,但它还可以用渐近表达式表征。这充分说明渐近段的特殊性。渐近段的特殊性,植根于应力奇异性。
渐近段界面剪应力的分布由渐近表达式(22)表征。渐近表达式中的参变数只有二个,即奇异性指数和应力强度因子 。 。 仅依赖于由结构决定的参数 仅依赖于由结构决定的参数 和 和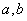 ,与外力的作用无关, ,与外力的作用无关, 可称为结构参量。 可称为结构参量。 的值由外力决定, 的值由外力决定, 是力学参量。在渐近表达式中, 是力学参量。在渐近表达式中, 决定界面剪应力按 决定界面剪应力按 的规律分布, 的规律分布, 和 和 的乘积确定渐近段内界面剪应力的渐近值。无论外力如何改变,它只影响 的乘积确定渐近段内界面剪应力的渐近值。无论外力如何改变,它只影响 的数值,界面剪应力也随着 的数值,界面剪应力也随着 按比例变化,却不会改变渐近段界面剪应力按 按比例变化,却不会改变渐近段界面剪应力按 的分布规律。这种界面剪应力奇异分布的规律从奇点开始,一直保持到转换点,其影响范围遍及渐近段,反映了应力奇异性的存在。 的分布规律。这种界面剪应力奇异分布的规律从奇点开始,一直保持到转换点,其影响范围遍及渐近段,反映了应力奇异性的存在。
渐近段界面剪应力的规律具有深刻的内涵。界面端点是界面剪应力的一个奇点,界面端点处,界面剪应力趋于无限大。在转换点,界面剪应力急剧降至 。在端点至转换点的范围内,有了任何一点的坐标值和相应的界面剪应力值,就可以根据渐近表达式推算出应力强度因子。当然,也可以推算出任意另外一点的界面剪应力值,包括端点和渐近点。这说明已知渐近段内的任意一点及其界面剪应力,就可以确定出整个渐近段的界面剪应力。 。在端点至转换点的范围内,有了任何一点的坐标值和相应的界面剪应力值,就可以根据渐近表达式推算出应力强度因子。当然,也可以推算出任意另外一点的界面剪应力值,包括端点和渐近点。这说明已知渐近段内的任意一点及其界面剪应力,就可以确定出整个渐近段的界面剪应力。
渐近段内不同点的界面剪应力,不论是无限大还是有限大,不论是较大还是较小,它们都对应于同一个应力强度因子,而是用作控制界面端点处初始脱粘是否发生的力学参量 [7]。由此可见,渐近段内不同点的界面剪应力不能再用作控制界面端点处初始脱粘是否发生的力学参量。换言之,渐近段内的界面剪应力不具有物理灵敏性。这种情形使得我们没有办法以一般的应力场来看待渐近段的奇异应力场。
6 渐近段界面剪应力的非奇异分布
渐近段界面剪应力奇异分布的规律是应力奇异性造成的。我们不能以一般的应力场来看待渐近段奇异分布的界面剪应力。那么,渐近段内能否找到按非奇异分布的界面剪应力呢?这里,非奇异分布的界面剪应力是指未受奇异性干扰,不按规律分布的界面剪应力。
基本段的界面剪应力是一般的应力场,具有物理灵敏性,是非奇异分布的界面剪应力,可以用作控制界面初始脱粘是否发生的力学参量[15]。转换点是渐近段和基本段的连接处,是基本段的非奇异分布和渐近段的奇异分布的过渡点。因此,转换点可以作为考察渐近段内的界面剪应力的非奇异分布的出发点。
在还没有关于渐近段内的界面剪应力的非奇异分布的可靠分析前,我们可以作如下的定性估计。由于转换点的位置非常靠近自由边界,其间的距离通常以微米度量,将基本段的界面剪应力自转换点外插到界面端点,可以作为渐近段内非奇异分布界面剪应力的近似。由此可以得到界面端点处的非奇异分布的界面剪应力的近似值。以B1到B6为例,用外插法得到的界面端点处的非奇异分布的界面剪应力既不是零,也不是无限大物理论文,而是一个与转换点界面剪应力相近的有限值。
那么,为什么在半平面双材料角B1到B6的弹性力学严格解中,我们看不到这种渐近段的非奇异分布的界面剪应力呢?这是因为对于B1到B6,如果界面端点处的非奇异分布的界面剪应力是有限值,就会在端点产生应力奇异性。
7 半平面双材料角端点存在应力奇异性的条件
考虑到有的半平面双材料角在端点出现应力奇异性,如B1到B6,而另外的半平面双材料角的端点处不出现应力奇异性,如B7。由此可见,半平面双材料角界面端点本身并非一定是界面应力的奇点,要使得端点变成界面应力的奇点,必有别的附加条件。
半平面双材料角B7与B1到B6的些微差别表现在端点的非奇异分布的界面剪应力上。B7( )的端点的非奇异分布的界面剪应力为零(见图3),而B1到B6( )的端点的非奇异分布的界面剪应力为零(见图3),而B1到B6( )的端点的非奇异分布的界面剪应力是一个与转换点界面剪应力相差不大的有限值(近似插值,见节7)。根据剪应力互等定理,由于在自由边界的端点处,给定的剪应力为零,所以要求端点处的界面上的剪应力也必须是零。B1到B6的端点的非奇异分布的界面剪应力等于有限值,而在自由边界的端点处,给定的剪应力为零,这使得剪应力互等定理在界面端点得不到满足。于是B1到B6的端点成为边界条件的一个奇点,端点处的应力奇异性由此产生。结果是:在存在边界条件奇点的严格解中,出现渐近段内界面剪应力按规律的奇异分布。 )的端点的非奇异分布的界面剪应力是一个与转换点界面剪应力相差不大的有限值(近似插值,见节7)。根据剪应力互等定理,由于在自由边界的端点处,给定的剪应力为零,所以要求端点处的界面上的剪应力也必须是零。B1到B6的端点的非奇异分布的界面剪应力等于有限值,而在自由边界的端点处,给定的剪应力为零,这使得剪应力互等定理在界面端点得不到满足。于是B1到B6的端点成为边界条件的一个奇点,端点处的应力奇异性由此产生。结果是:在存在边界条件奇点的严格解中,出现渐近段内界面剪应力按规律的奇异分布。
对于双材料角B7,端点处没有剪应力互等定理的矛盾,所以不是边界条件的奇点。
半平面双材料角端点存在应力奇异性的条件归结为:1)应力奇异性指数 ,2)在界面端点处,给定的边界剪应力为零,3)在界面端点处,非奇异分布的界面剪应力是有限值。应力奇异性指数 ,2)在界面端点处,给定的边界剪应力为零,3)在界面端点处,非奇异分布的界面剪应力是有限值。应力奇异性指数 是半平面双材料角应力奇异性的必要条件,剪应力互等定理在界面端点无法满足是半平面双材料角应力奇异性的充分条件。 是半平面双材料角应力奇异性的必要条件,剪应力互等定理在界面端点无法满足是半平面双材料角应力奇异性的充分条件。
4/5 首页 上一页 2 3 4 5 下一页 尾页 |


