论文导读::本文对半平面双材料角受集中力问题的界面应力场作了深入的探究,特别着重于双材料角端点附近的界面应力的奇异性分布规律。
论文关键词:双材料角,应力奇异性,界面应力,应力强度因子
0 引言
自上世纪八十年代以来,对于双材料角的初始脱粘判据的研究,主要是按照断裂力学[1]的思路进行的,即采用双材料角应力强度因子作为界面强度参数。迄今的研究表明,用双材料角应力强度因子只能建立固定楔角的双材料角的初始脱粘判据,不能用来建立适用于不同楔角的双材料角的初始脱粘的一般判据。为了探索建立不同楔角的双材料角的初始脱粘的一般判据的途径,有必要对双材料角端点附近的界面应力的奇异性分布作深入的研究,藉以求得对双材料角应力奇异性的内禀特性的充分了解。
Williams [2]发现在双材料界面的自由边界处存在应力奇异性,而奇异性应力可以用下式表示:
 ????????(1) ????????(1)
其中 表示界面应力, 为场点至界面端点的距离, 为场点至界面端点的距离, 称为应力强度因子,而 称为应力强度因子,而 则是应力奇异性指数。 则是应力奇异性指数。
Bogy [3-4],Hein [5]采用Airy应力函数和Mellin变换,求解了双材料角的平面特征值问题,得到的奇异性指数 不是常数,而是与Dundurs常数及双材料角的二个楔角有关的函数,即 不是常数,而是与Dundurs常数及双材料角的二个楔角有关的函数,即
 (2) (2)
式中Dundurs常数是二种材料的四个弹性常数的组合[6]
(3)
(4)
式中 为剪切模量,为Poisson比,下标1,2标注二种不同材料。 为剪切模量,为Poisson比,下标1,2标注二种不同材料。
由于 , , ,Dundurs常数只能在()坐标平面上的以(1, 0),(1, 0.5),(-1, 0)和(-1, -0.5)为顶点的平行四边形内取值。 ,Dundurs常数只能在()坐标平面上的以(1, 0),(1, 0.5),(-1, 0)和(-1, -0.5)为顶点的平行四边形内取值。
双材料角的奇异性指数一般以复数的形式来表示: 。根据 。根据 和 和 的值,双材料角可分为三种情形: 的值,双材料角可分为三种情形:
(1) 无奇异性 ( ), ),
(2) 奇异性 ( ), ),
(3) 振荡奇异性 ( ). ).
在许多新型材料和结构中常常会遇到双材料角,例如:复合材料,焊接结构,倒装芯片的封装等。由于双材料角的奇异应力场可能导致界面的脱粘,所以是否会发生双材料角初始脱粘的判定格外重要。从Gradin [7], Akisanya[8], Reedy [9], Labossiere [10]和Nied [11]等文献中,可以看到采用双材料角应力强度因子作为界面强度参数,来建立固定楔角的双材料角奇异性初始脱粘判据的研究进展。Mohammed [12] 试图采用内聚力模型来建立适用于不同楔角的双材料角的初始脱粘的一般判据,他们得到的是预测失效载荷的一个由特别的设计参数表示的经验公式,不能称之为一般判据。所以,适用于不同楔角的双材料角的初始脱粘的一般判据至今尚未建立起来。
Sinclair [13-14]对双材料角的应力奇异性的研究和进展作了全面的综述。他指出如果要把应力分析方法应用于建立双材料角奇异性初始脱粘的一般判据,可以有如下的二个选择。其一是尝试除去应力奇异性以获得物理灵敏性的应力(physically sensitive stress)。其二是对应力奇异性赋以准确的物理意义的说明。至于怎样做到这二个选项的要求,文中没有论述。
Dai [15]对半平面双材料角受集中力问题 [16] 的严格解和渐近解的界面奇异应力场进行了研究,得到的结果是:如果应力奇异性指数较高,双材料角初始脱粘可能发生在双材料角的端点处,如果应力奇异性指数较低,则双材料角初始脱粘将不发生在双材料角的端点处,而是发生在离端点较远的界面应力的极大值处。这个结果得到了实验的证实[17-18]。
对双材料角界面应力场奇异性的内禀特性的充分了解是建立双材料角奇异性初始脱粘一般判据的理论基础。虽然渐近解给出应力强度因子,并能表示界面应力奇异性分布的主要特点,但它只是奇异性界面应力的渐近表达。所以要获得关于奇异性界面应力场的透彻的了解,同时考察严格解和渐近解是必要的。渐近解以应力强度因子表示应力奇异性,严格解以应力分量表示应力奇异性。要了解双材料角界面应力场奇异性的内禀特性,除了考察严格解和渐近解之外,没有别的途径。
本文对半平面双材料角受集中力问题[16]的界面应力的严格解和渐近解作了深入的探究,特别着重于双材料角端点附近的界面应力的奇异性分布规律。通过对严格解和渐近解的比较,探求对半平面双材料角应力奇异性的内禀特性的透彻了解。这是探索建立不同楔角的双材料角初始脱粘的一般判据的可行途径。
1半平面双材料角受集中力问题
半平面双材料角受集中力的弹性力学边值问题如图1所示。取极坐标( ),坐标原点与双材料角的界面端点重合, ),坐标原点与双材料角的界面端点重合,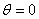 面为界面。集中力 面为界面。集中力 作用在边界上,作用点离双材料角的端点的距离为 作用在边界上,作用点离双材料角的端点的距离为 。 。
Bogy [16] 采用Airy应力函数和Mellin变换,求得了半平面双材料角受集中力的弹性力学边值问题的严格解和渐近解。
1.1 界面剪应力与正应力的严格解
令tij (r, q)表示极坐标中的应力分量, 表示无量纲坐标:。无量纲界面剪应力和界面应力分别记作 表示无量纲坐标:。无量纲界面剪应力和界面应力分别记作 和 和 。Bogy给出 。Bogy给出 和 和 的严格解(rigorous solution)的积分表达式如下[16]: 的严格解(rigorous solution)的积分表达式如下[16]:
1/5 1 2 3 4 5 下一页 尾页 |


