半平面双材料角界面应力奇异性分布规律的探究_物理论文

Fig. 5 Transition point of interfacial shear stress (_¨)

图 6 界面正应力曲线上的转换点(_¨)

Fig. 6Transition point of interfacial normal stress (_¨)

需要强调说明的一点是：转换点（Transition point）是客观存在的。按理，转换点应该用严格解和渐近解组成的联立方程，通过严格的数学分析来求出。但是，由于式（8）中包含有积分，这几乎是不可能的。因此，本文采用的是根据附表A的的数据，通过插值法求零点而得到。由于采用了数值积分和通过插值求零点位置，计算误差在所难免，但数值误差不能成为怀疑转换点存在的客观性的理由。这是因为虽然是二个大数相减得到的非常小的数，由于Maple 7的数值积分得到的界面应力有8位有效位数，能保证有足够的有效位数。所以，数值误差对振荡衰减正负相间的的影响很小，不会使求出的转换点失去真实性。

由附表A可以看到，在奇点附近 的变化同样有正负相间，向奇点逐渐衰减的振荡现象，所以也存在唯一的衰减的振荡现象在此突然消失的零点，即转换点。与并不重合。双材料角B1到B6的界面正应力的转换点的位置在图6中用_¨标出。图中，实线是严格解，虚线是渐近解。由于是负值，纵坐标轴未采用对数形式。

在区间内，图7中给出了B4，B5和B6的曲线。相对于界面剪应力，曲线的幅值很小，而且衰减得很快，是向奇点衰减的微幅振荡函数。

在转换点至无穷远的区间内，渐近解显著地偏离严格解，所以渐近解应该被舍弃不用。根据同样的理由，在转换点至无穷远的区间内，差值和也应该被舍弃不用。换言之，和的定义域分别是 。于是根据转换点的定义，式（17）和（18）可以改写成：

（19）

（20）

图7, 双材料角 B4-B6的D_t 曲线

图 7 渐近段内双材料角的严格解与渐近解之差

Fig. 7Difference D_t of bimaterial corners B4 to B6

界面剪应力曲线上的转换点的剪应力和正应力分别记作和，的最大幅值记作，转换点的坐标记作。双材料角B1到B6的，，，和的数值列于表2。作为比较，界面剪应力的极大值（在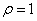的附近）也在表2中给出。从表2看到：(D_t)_max 与相比，是一个可以忽略的小的数值。此外，值得注意的一点是：随着的提高而提高，而对的影响较小。从表2看到：B1到B3的大于，伴随着奇异性指数的增大，B4到B6?的大于cssci期刊目录。

有与 类似的情况，见表3。界面正应力曲线上的转换点的剪应力和正应力分别记作和，的最大幅值记作。从表2和表3看到，B1到B6的界面正应力的转换点分别在对应的界面剪应力的转换点的靠近端点的一侧。

表2 双材料角B1到B6的剪应力曲线上的转换点

Asymptoticpoints on interfacial shear stress of B1 to B6

table2表3 双材料角B1到B6的正应力曲线上的转换点

Asymptoticpoints on interfacial normal stress of B1 to B6

table34 渐近段的渐近表达式

界面剪应力的转换点是向端点作微幅震荡衰减的的起始点，当自转换点减小到零，渐近解是以的微幅震荡衰减的方式来和严格解趋近的。所以，自奇点到转换点，这一段可以称为渐近段。在自奇点到转换点的渐近段内，式（19）成立，并可改写成

(21)

由式（21）可见，自渐近段内，严格解等于渐近解与之和。由于在整个渐近段范围内，与相比，只是一个小量。若允许有的误差，则在渐近段内严格解可以用渐近解来近似，并表示如下

 3/5   首页 上一页 1 2 3 4 5 下一页 尾页