 (5) (5)
 (6) (6)
其中
 (7) (7)
(8)
 ,(9) ,(9)
 
图 1 二个1/4平面粘合的双材料角受集中力
Fig. 1Scheme of edge-bonded quarter-planes under concentrated normal force
由于严格解中包含有由Mellin反变换所带来的积分(见式(8)),所以对界面剪应力和界面正应力的分布规律的研究,只能通过数值积分来完成。
1.2 界面剪应力与正应力的渐近解
在严格解的基础上,Bogy还给出了界面剪应力和界面正应力的渐近解(asymptotic solution),其公式由(10)至(14)给出[16]:
 (10) (10)
 (11) (11)
 (12) (12)
 , (13) , (13)
 , (14) , (14)
式中,符号^表示渐近解, 是在-1到-2之间的一个零点。 是在-1到-2之间的一个零点。
对于给定的半平面双材料角,已知其Dundurs常数,,由式(10)到式(14),可得界面剪应力和正应力的渐近解的解析表达式如下:???????
 (15) (15)
 (16) (16)
式中: 是奇异性指数, 是奇异性指数, 和 和 分别为界面剪应力和界面正应力的应力强度因子,由公式(10)到(14)确定。 分别为界面剪应力和界面正应力的应力强度因子,由公式(10)到(14)确定。
半平面双材料角的应力奇异性指数与双材料的Dundurs常数 的关系见图2。由图中的等值线可见,半平面双材料角的应力奇异性指数的值可能是零,或者是一个小于1的正实数。 的关系见图2。由图中的等值线可见,半平面双材料角的应力奇异性指数的值可能是零,或者是一个小于1的正实数。
图 2 半平面双材料角的奇异性指数 [4]
Fig. 2 Singularity exponents ofedge-bonded quarter-planes [4]
2 界面剪应力与正应力的分布
Bogy在[16]的图10-11中,给出了六种半平面双材料角的界面剪应力与正应力的分布曲线作为示例,其中三种有奇异性,另外三种没有奇异性。图中界面应力曲线的数据点的范围大约在 之间,文中没有对界面应力的分布规律进行讨论。 之间,文中没有对界面应力的分布规律进行讨论。
根据本文研究的需要,另选B1到B7七种双材料。在表1中给出了这七种半平面双材料角的Dundurs常数,奇异性指数,界面剪应力和界面正应力的应力强度因子 和 和 。这七种半平面双材料角的奇异性指数分布在0到0.3839的范围内。 。这七种半平面双材料角的奇异性指数分布在0到0.3839的范围内。
双材料角B1到B7的严格解的界面剪应力和界面正应力物理论文,用公式(5)到(9)计算,全部数值计算用Maple 7 [19] 完成。Maple 7能够完成式(8)中的积分,并得出足够准确的数值结果。为了能够考察双材料角端点附近的界面应力的分布,数据点自非常小的数 开始,一直计算到 开始,一直计算到 。在 。在 的范围内,数据点还需加密到足以显示出界面应力的奇异性分布的主要性态。 的范围内,数据点还需加密到足以显示出界面应力的奇异性分布的主要性态。
双材料角B1到B7的渐近解的界面剪应力和界面正应力,用公式(15),(16)计算,计算中数据点的选取与严格解相同。
双材料角B1到B7的严格解和渐近解的界面剪应力和界面正应力分别以实线和虚线绘出在图3和图4中。
由图3,图4可见,B1到B7的严格解的界面剪应力和界面正应力分别在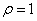 , , 附近达到极大值。B7没有奇异性,在端点处,界面剪应力为零,界面正应力取有限值。B1到B6都有奇异性,当 附近达到极大值。B7没有奇异性,在端点处,界面剪应力为零,界面正应力取有限值。B1到B6都有奇异性,当 ,界面剪应力和界面正应力都趋于无限大。在 ,界面剪应力和界面正应力都趋于无限大。在 及其邻近,渐近解和严格解逐渐趋近。随着奇异性指数 及其邻近,渐近解和严格解逐渐趋近。随着奇异性指数 的减小,B6到B1的靠近端点的曲线段依次向纵坐标轴靠近。 的减小,B6到B1的靠近端点的曲线段依次向纵坐标轴靠近。
表 1 双材料角B1到B7的Dundurs 常数,奇异性指数和应力强度因子
|
双材料角
|
?
|

|
?
|

|

|
|
B1
|
-0.5
|
0
|
0.1468
|
0.03404
|
-0.1210
|
|
B2
|
-0.6
|
0
|
0.1940
|
0.04298
|
-0.1311
|
|
B3
|
-0.7
|
0
|
0.2436
|
0.05247
|
-0.1409
|
|
B4
|
-0.8
|
0
|
0.2952
|
0.06294
|
-0.1513
|
|
B5
|
-0.9
|
0
|
0.3489
|
0.07502
|
-0.1632
|
|
B6
|
-0.98
|
0
|
0.3839
|
0.08640
|
-0.1745
|
|
B7
|
-0.5
|
-0.25
|
0
|
-
|
-
|
Bimaterial corners B1 to B7 and parameters in asymptoticexpressions
table13 奇点附近严格解与渐近解的比较
半平面双材料角B1到B6的端点是界面应力的奇点,但是在图3和图4上,无法看清楚严格解和渐近解的界面应力在奇点附近是如何相互趋近的。要看清楚严格解和渐近解的界面应力在奇点附近是如何相互趋近的,就是要知道 和 和 在奇 在奇
点附近的变化。这里, 和 和 分别表示界面剪应力和界面正应力的严格解和渐近解在奇点附近的差值。 分别表示界面剪应力和界面正应力的严格解和渐近解在奇点附近的差值。
 (17) (17)
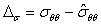 (18) (18)
图 3 界面剪应力(实线为严格解,虚线为渐近解)
Fig. 3 Interfacial shear stress
(solid line: rigorous solution, dashed line: asymptotic solution)
图 4 界面正应力(实线为严格解,虚线为渐近解)
Fig. 4 Interfacial normal stress
(solid line: rigorous solution, dashed line: asymptotic solution)
在奇点附近, 和 和 的数值非常小,B4到B6的和 的数值非常小,B4到B6的和 列出在本文附录的附表A中。由附表A可以看到,在奇点附近的变化有正负相间,向奇点衰减的振荡现象;在每一次正负变号的地方,一定有一个 列出在本文附录的附表A中。由附表A可以看到,在奇点附近的变化有正负相间,向奇点衰减的振荡现象;在每一次正负变号的地方,一定有一个 的零点。 的零点。 的零点也就是严格解和渐近解的交点。在某一个零点的外面,衰减的振荡现象突然消失。由附表A可见,Dt 的零点不是唯一的,但是衰减的振荡现象在此突然消失的零点却是唯一的。这个唯一的零点,具有特殊的意义,定名为转换点(Transition point)。转换点是衰减的振荡应力的起始点,其坐标用 的零点也就是严格解和渐近解的交点。在某一个零点的外面,衰减的振荡现象突然消失。由附表A可见,Dt 的零点不是唯一的,但是衰减的振荡现象在此突然消失的零点却是唯一的。这个唯一的零点,具有特殊的意义,定名为转换点(Transition point)。转换点是衰减的振荡应力的起始点,其坐标用 表示。双材料角B1到B6的界面剪应力的转换点的位置在图5中用¨标出。图5的坐标轴采用对数形式,图中,实线是严格解,虚线是渐近解。 表示。双材料角B1到B6的界面剪应力的转换点的位置在图5中用¨标出。图5的坐标轴采用对数形式,图中,实线是严格解,虚线是渐近解。
2/5 首页 上一页 1 2 3 4 5 下一页 尾页 |


