论文导读::PCA/DEA复合模型在医院相对效率评价中的应用,数学建模论文。
论文关键词:主成分分析,数据包络分析,相对效率
1引言
卫生资源配置效率问题成为目前医疗卫生领域关注的焦点问题之一.目前,从医院管理的角度看,对医院进行绩效评价的方法有不少,但是这些方法主要是从医院自身出发,从组织内部的角度进行绩效评价的.从整个医疗行业这个外部环境来看,对每家医院同其他医院进行效率比较的研究目前在国内还比较少.Berger与Humphrey在对金融机构的效率研究中总结了效率研究方法主要分为参数法和非参数法两大类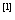 .其中,参数法包括SFA(StochasticFrontier Approach)、DFA(Distribution Free Approach)和TFA(Thick Frontier Approach)三种,非参数法包括DEA(Data Envelopment Analysis)和FDH(Free Disposal Hull)两种,并认为SFA和DEA是更好的两种效率测量方法 .其中,参数法包括SFA(StochasticFrontier Approach)、DFA(Distribution Free Approach)和TFA(Thick Frontier Approach)三种,非参数法包括DEA(Data Envelopment Analysis)和FDH(Free Disposal Hull)两种,并认为SFA和DEA是更好的两种效率测量方法 .随后Ondrich & Ruggiero和Ruggiero分别利用SFA和DEA对截面数据和面板数据的对比分析后发现SFA比DEA并不具备任何分析优势,反而由于DEA具有非参数性和支持多变量输入输出的特性而得到广泛应用 .随后Ondrich & Ruggiero和Ruggiero分别利用SFA和DEA对截面数据和面板数据的对比分析后发现SFA比DEA并不具备任何分析优势,反而由于DEA具有非参数性和支持多变量输入输出的特性而得到广泛应用 . .
另外,医院绩效评价是一种典型的多指标问题,涉及的因素繁多.多指标带来了分析上的复杂性和指标间的多重相关性两大问题.医院绩效评价的各个指标之间往往是相互关联,相互制约的,这种相关性使得观测数据在一定程度上反映的信息有所重叠,可以采用主成分分析法(Principal Components Analysis, PCA)对原始指标体系进行化简,将投入和产出指标进行多指标综合,以使评价指标降维,从而实现用少数几个综合指标代替原始众多指标 .为此,笔者在分析和构建一套合理的医院绩效评价指标体系的基础上,提出了一种基于PCA/DEA 的复合评价模型,进而为医院相对效率评价提供了一种有效的方法. .为此,笔者在分析和构建一套合理的医院绩效评价指标体系的基础上,提出了一种基于PCA/DEA 的复合评价模型,进而为医院相对效率评价提供了一种有效的方法.
2 效率评价指标体系构建
本文选取湖南省35家大型综合医院为决策单元(DecisionMaking Unit, DMU),基于医院资料取得的限制及多数学者采用的输入与产出项,选取医师数,护士数,病床数,其他医疗人员,护医比,护床比,固定资产,医院成本,床均固定资产九项为投入变量;门急诊人次,住院人次,手术次数,每医生年均负责急诊人次数,每医生日均负责急诊人次数,医院收入,盈利,固定资产产值率八项为产出项.采用SAS9.1.3软件,运用PCA法对35家医院2004年统计数据进行指标压缩得到如下(表1-表4).
表1 投入指标的总方差分解表
|
相关矩阵特征值
|
因子提取结果
|
|
|
Eigenvalue
|
Proportion
|
Cumulative
|
Eigenvalue
|
Proportion
|
Cumulative
|
|
1
|
5.80720912
|
0.6452
|
0.6452
|
5.80720912
|
0.6452
|
0.6452
|
|
2
|
1.50615550
|
0.1674
|
0.8126
|
1.50615550
|
0.1674
|
0.8126
|
|
3
|
0.78769761
|
0.0875
|
0.9001
|
|
|
|
|
4
|
0.54793649
|
0.0609
|
0.9610
|
|
|
|
|
5
|
0.19932715
|
0.0221
|
0.9831
|
|
|
|
|
6
|
0.08308800
|
0.0092
|
0.9924
|
|
|
|
|
7
|
0.03499355
|
0.0039
|
0.9963
|
|
|
|
|
8
|
0.02404576
|
0.0027
|
0.9989
|
|
|
|
|
9
|
0.00954683
|
0.0011
|
1.0000
|
|
|
|
| |
|
|
|
|
|
|
|
表2 旋转后的因子荷载矩阵
|
Prin
|

|

|

|

|

|

|

|

|

|
|

|
0.389134
|
0.395336
|
0.368886
|
0.379902
|
-0.05739
|
0.057565
|
0.395271
|
0.399562
|
0.298972
|
|

|
-0.14070
|
-0.04744
|
-0.084450
|
0.224927
|
0.595688
|
0.705995
|
-0.02236
|
-0.117600
|
0.229401
|
表3 产出指标的总方差分解表
|
相关矩阵特征值
|
因子提取结果
|
|
|
Eigenvalue
|
Proportion
|
Cumulative
|
Eigenvalue
|
Proportion
|
Cumulative
|
|
1
|
3.95731318
|
0.4947
|
0.4947
|
3.95731318
|
0.4947
|
0.4947
|
|
2
|
1.63003331
|
0.2038
|
0.6984
|
1.63003331
|
0.2038
|
0.6984
|
|
3
|
0.93631283
|
0.1170
|
0.8155
|
0.93631283
|
0.1170
|
0.8155
|
|
4
|
0.77849056
|
0.0973
|
0.9128
|
|
|
5
|
0.60115040
|
0.0751
|
0.9879
|
|
|
6
|
0.05846612
|
0.0073
|
0.9952
|
|
|
7
|
0.03823275
|
0.0048
|
1
|
|
|
8
|
0.00000084
|
0.0000
|
1
|
|
表4 旋转后的因子荷载矩阵
|
Prin
|

|

|

|

|

|

|

|

|
|
1
|
0.48429
|
0.236659
|
0.438295
|
0.383426
|
0.383466
|
0.431459
|
0.168928
|
0.092715
|
|
2
|
-0.078051
|
-0.428572
|
-0.308914
|
0.437496
|
0.437416
|
-0.29321
|
0.125145
|
0.480037
|
|
3
|
0.029105
|
-0.118886
|
0.050002
|
-0.24274
|
-0.242517
|
0.08425
|
0.908836
|
0.178048
|
分别选取投入部分的第一、第二主成分( , , )作为投入指标以及产出部分的第一、第二、第三主成分( )作为投入指标以及产出部分的第一、第二、第三主成分( )作为产出指标. 根据PCA法压缩指标的结果,分别计算出压缩后35家医院的两个投入指标和三个产出指标的值.由于该投入、产出变量的数值不能满足DEA模型对 )作为产出指标. 根据PCA法压缩指标的结果,分别计算出压缩后35家医院的两个投入指标和三个产出指标的值.由于该投入、产出变量的数值不能满足DEA模型对 , , 的要求,需要对变量加以修正.因此可对非全正数投入和产出以及产出指标综合评价值作如下线性处理: 的要求,需要对变量加以修正.因此可对非全正数投入和产出以及产出指标综合评价值作如下线性处理:
 ; ;
其中 表示正向化后的投入指标值, 表示正向化后的投入指标值, 表示第 表示第 家医院的第 家医院的第 个投入指标值; 个投入指标值; 表示正向化后的产出指标值, 表示正向化后的产出指标值, 表示第 表示第 家医院的第 家医院的第 个产出指标值.经过公式变换后 个产出指标值.经过公式变换后 .将经线性变化后的指标作为最终的投入、产出指标(表5). .将经线性变化后的指标作为最终的投入、产出指标(表5).
表5 最终投入、产出数据指标
|
|
X1
|
X2
|
Y1
|
Y2
|
Y3
|
|
DMU 1
|
0.2260
|
0.2408
|
0.1286
|
0.1185
|
0.1255
|
|
DMU 2
|
0.3395
|
0.5114
|
0.4959
|
0.2432
|
0.3409
|
|
DMU 3
|
1.0000
|
0.9702
|
1.0000
|
0.4931
|
1.0000
|
|
DMU 4
|
0.2532
|
0.2949
|
0.1855
|
0.1700
|
0.1524
|
|
DMU 5
|
0.1298
|
0.1514
|
0.1997
|
0.1000
|
0.1000
|
|
DMU 6
|
0.1989
|
0.2611
|
0.1924
|
0.1611
|
0.1619
|
|
DMU 7
|
0.3128
|
0.3937
|
0.1439
|
0.1844
|
0.2719
|
|
DMU 8
|
0.4249
|
0.4614
|
0.2913
|
0.2620
|
0.4729
|
|
DMU 9
|
0.1158
|
0.1920
|
0.1449
|
0.1129
|
0.1582
|
|
DMU 10
|
0.1014
|
0.2692
|
0.3039
|
0.1772
|
0.3897
|
|
DMU 11
|
0.2721
|
0.2976
|
0.2062
|
0.1930
|
0.2148
|
|
DMU 12
|
0.6571
|
1.0000
|
0.9755
|
0.4726
|
0.9818
|
|
DMU 13
|
0.3769
|
0.2353
|
0.1230
|
0.1434
|
0.1338
|
|
DMU 14
|
0.2523
|
0.3707
|
0.3730
|
0.1706
|
0.1853
|
|
DMU 15
|
0.2518
|
0.2868
|
0.3789
|
0.2200
|
0.2520
|
|
DMU 16
|
0.3616
|
0.3057
|
0.2634
|
0.2071
|
0.1614
|
|
DMU 17
|
0.3548
|
0.4938
|
0.5675
|
0.2860
|
0.4207
|
|
DMU 18
|
0.2242
|
0.2868
|
0.1681
|
1.0000
|
0.3000
|
|
DMU 19
|
0.2441
|
0.4113
|
0.2425
|
0.1782
|
0.2696
|
|
DMU 20
|
0.2012
|
0.3490
|
0.2332
|
0.1988
|
0.2793
|
|
DMU 21
|
0.3643
|
0.5209
|
0.6109
|
0.3191
|
0.3243
|
|
DMU 22
|
0.1000
|
0.1000
|
0.1000
|
0.1048
|
0.1022
|
|
DMU 23
|
0.1881
|
0.2259
|
0.2060
|
0.1714
|
0.2121
|
|
DMU 24
|
0.2509
|
0.5006
|
0.4835
|
0.2649
|
0.2951
|
|
DMU 25
|
0.2889
|
0.4316
|
0.4337
|
0.2626
|
0.3305
|
|
DMU 26
|
0.2441
|
0.3328
|
0.2696
|
0.1865
|
0.2055
|
|
DMU 27
|
0.2712
|
0.3517
|
0.2769
|
0.2397
|
0.2817
|
|
DMU 28
|
0.2441
|
0.3369
|
0.3309
|
0.2380
|
0.3089
|
|
DMU 29
|
0.4348
|
0.6332
|
0.7461
|
0.3506
|
0.4723
|
|
DMU 30
|
0.2667
|
0.3815
|
0.2847
|
0.1912
|
0.1995
|
|
DMU 31
|
0.2373
|
0.4356
|
0.3258
|
0.1895
|
0.2064
|
|
DMU 32
|
0.2852
|
0.3761
|
0.2535
|
0.2307
|
0.2556
|
|
DMU 33
|
0.1628
|
0.2272
|
0.1812
|
0.1263
|
0.1055
|
|
DMU 34
|
0.3679
|
0.4343
|
0.4419
|
0.2598
|
0.2536
|
|
DMU 35
|
0.2667
|
0.2584
|
0.1795
|
0.1840
|
0.1693
|
3 DEA模型基本原理
 原始模型是计算产出与投入之比的最大值,为了求解方便,Charnes等在研究过程中将分式规划问题转换成线性规划的对偶问题,并通过引进非阿基米德无穷小的概念,成功解决了计算上和技术上的困难. 原始模型是计算产出与投入之比的最大值,为了求解方便,Charnes等在研究过程中将分式规划问题转换成线性规划的对偶问题,并通过引进非阿基米德无穷小的概念,成功解决了计算上和技术上的困难.

其中 表示产出指标, 表示产出指标, 表示投入指标, 表示投入指标, 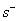 、 、 分别表示投入过剩和产出不足, 分别表示投入过剩和产出不足, 称为固定规模报酬的技术效率( Technical Efficiency from Constant Return to Scale),取值范围在 称为固定规模报酬的技术效率( Technical Efficiency from Constant Return to Scale),取值范围在 之间, 之间, 是非阿基米德无穷小,一般取 是非阿基米德无穷小,一般取 .其经济意义为: .其经济意义为:
若 ,则DUM是弱有效,其意义就是DUM的生产活动不同时具有技术有效和规模有效.如果某个 ,则DUM是弱有效,其意义就是DUM的生产活动不同时具有技术有效和规模有效.如果某个 ,表示该种输入要素有 ,表示该种输入要素有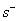 个单位没有被充分利用,如果 个单位没有被充分利用,如果 ,表示实际输出与理论输出有 ,表示实际输出与理论输出有 个单位的差距,也就是输出不足;若 个单位的差距,也就是输出不足;若 ,且 ,且 ,则决策单元是有效的,表示决策单元的活动同时技术有效和规模有效,各种资源得到了充分利用,取得了最大的输出效果;若 ,则决策单元是有效的,表示决策单元的活动同时技术有效和规模有效,各种资源得到了充分利用,取得了最大的输出效果;若 ,则说明决策单元不是DEA有效的,它的生产活动既不是技术有效,也不是规模有效. ,则说明决策单元不是DEA有效的,它的生产活动既不是技术有效,也不是规模有效.
1/2 1 2 下一页 尾页 |


