论文导读:：本文对固体废弃物填埋场建立了二维饱和－非饱和渗流数学模型，对固体废弃物填埋场内部渗流场进行了研究。在以总压力水头为未知量的多孔介质三维饱和－非饱和渗流方程基础上，将饱和、非饱和区域视为一个整体来进行研究，建立了以显式格式和有限体积法（FVM）为基础的二维饱和－非饱和渗流模型，并运用于深圳市下坪固体废弃物填埋场内部渗流场的计算。
论文关键词：填埋场，饱和，非饱和，渗流，有限体积法
1 引言
由于经济快速发展，城市化扩大，居民消费水平日益提高，我国城市垃圾处置及污染防治已成为环境保护的突出问题。其中有关固体废弃物污染地下水的事故屡有发生。］渗滤液对含水层的影响不仅限于表层，而且能影响到 60 m深的范围。渗滤液污染地下水的另一个特点是持续时间长，据研究报道，垃圾填埋场在封场后生物分解过程还会持续10～20年［1］饱和，在封场后70～上百年的时间仍可能有渗滤液的渗出。一旦地下水源和周围土壤被污染，想用人工方法实施再净化，技术上将十分困难，其费用也及其昂贵中国论文下载中心。
目前,国内外计算渗滤液的方法多为水量平衡法[2]，但该法没有考虑填埋场内水分的运动过程，计算出的渗滤液量偏高。本文基于地下水水力学理论，建立填埋场渗流数学模型，研究渗滤液产量的规律。
2 埋场饱和－非饱和渗流数学模型
2.1 饱和―非饱和地下水运动基本控制方程
首先建立一个描述整体区域的正交笛卡儿坐标系 ， 垂直向上。对于任意一种透水介质，设其空间三个正交主方向的透水系数为 ，下标 组成空间任意局部正交坐标系。在局部坐标系下，地下水流动的达西定律可表示为
 （公式1）
式中， 分别为方向的流速分量； 为总土水势， ； 为总土水势对于局部坐标的导数。经过转化及利用连续条件饱和，可以得到在整体坐标系下非均质非定常渗流方程为
 （公式2）
方程（公式2）为饱和－非饱和地下水流动的基本控制方程。 为时间， 为透水介质的孔隙率， 为含水率， 为比储流系数（＝ ）， 为比水分容量 , 为系数（ ，饱和区； ，非饱和区）， 为渗透系数，可表示为
 （公式3）
这里， 为式（公式3）定义的整体笛卡儿坐标下的介质在饱和状态下的渗透系数，只与土质的特性有关，与孔隙压力状态无关； 为相对渗透系数，是孔隙压力水头和含水率的函数[3]。
2.2数值求解
本文考虑的是垂向二维问题，且认为固体废弃物是各向同性的。因此饱和－非饱和地下水控制方程简化为：
 （公式4）
本文利用有限体积法求解饱和，经过简化，则得到最后的离散方程
 （公式5）
本文采用有结构网格，采用显式格式计算。
2.3计算参数处理
在实际工程中， ， 的函数关系一般是以试验离散点的形式给出，它们的函数关系可由离散点线性插值得来；的线性插值造成 阶梯状，在计算中将产生振荡，本文采用文献中对的处理方法[4]：
式中： 为本时间步的压力水头， 为上一时步的压力水头；
当 时， ， 由的离散点线性插值；
当 时， 。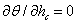
采用上述方法可有效的消除数值计算的振荡中国论文下载中心。
3 模型验证
3.1 计算条件
下坪固体废弃物填埋场位于深圳市布吉镇的上坪和下坪狭窄山谷中，三面环山，占地2240亩饱和，总库容约3000万立方米。主要处理罗湖、福田两区的城市生活垃圾。由于填埋场的整个区域比较规则，故选用矩形网格（图1）。
 图1 计算区域网格图
Fig 1 The grid of simulation area
3.1.1 初始条件
填埋场内部初始时刻为非饱和态，初始由重力势 和基质势 组成，基质势根据含水率由土壤水分曲线确定。由于缺乏固体废弃物水分曲线的实测数据，故本文根据固体废弃物的各种物理性质和别的土壤进行比对，选取类似的曲线来确定固体废弃物含水率和基质势的关系（图2）。
1/2 1 2 下一页 尾页 |
