论文摘要：为了研究非饱和土坡在降雨入渗条件下的稳定性，运用饱和-非饱和渗流有限元法模拟降雨条件下饱和-非饱和土坡暂态渗流场的变化情况，分析了降雨强度、降雨持时以及土壤饱和渗透系数等参数对非饱和土坡稳定性的影响。分析结果表明：土坡的安全系数随降雨强度的增大而增大，随饱和渗透系数的增大而减小。由于降雨的进行，雨水入渗量逐渐增加，基质吸力逐渐丧失，孔隙水压力逐渐增大，因而土坡的安全系数随降雨持时的增加而减小。
论文关键词：降雨,土坡稳定性,渗流,安全系数
引言
诱发边坡失稳的因素有很多，主要是降雨、地震、人类工程活动等。边坡中的渗透水压力和渗流场分布是影响边坡稳定和变形的重要因素之一，而降雨，特别是历时长、强度大的暴雨更是导致边坡失稳破坏的常遇诱导因素。以往的边坡渗流场研究通常采用稳定渗流模型，对降雨入渗补给的作用，仅考虑多年平均降雨量对应的入渗条件，且入渗边界假设在地下水面上，忽略降雨在非饱和区的运动过程。这种假设对于那些地下水位较高，非饱和带较浅的地区影响并不大；但对于地下水位较低，具有深厚非饱和区的边坡，则显得不尽合理。传统的边坡稳定分析方法也是建立在饱和土假设基础之上的，理论上忽略基质吸力对边坡稳定的贡献。这样的考虑是偏于安全，同时，也是由于非饱和土的研究还不够深入造成的。近年来，随着非饱和土力学的发展，为更加合理的进行边坡稳定分析提供了新的理论基础。
因此，本文考虑建立降雨入渗条件下的饱和-非饱和土坡计算模型，对雨水入渗引起的土坡安全系数下降进行定量分析，对于评估边坡的稳定性、预报滑坡灾害和边坡治理均具有重要的指导意义。
1饱和-非饱和渗流的控制方程
1.1饱和-非饱和渗流的控制方程及定解条件
饱和-非饱和渗流问题所满足的微分方程和边界条件为：
 (1)
式中：
S—水头分布规律已知的边界，H为边界水头，称为第一类边界条件；
S—流量情况己知的边界，q为单位时间边界法向流量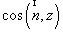， ， 为边界面外法线方向余弦，称为第二类边界条件；
S—渗出面边界，z为渗出面节点坐标，可以归为第一类边界条件；
H—初始渗流场水头，称为初始条件。
1.2Galerkin法有限元列式
将渗流场离散为有限个单元。假设单元内水头与结点水头的关系为：
 （2）
式中，N为单元形函数；n为单元节点数。
将式（2）代入式（1），并引入边界条件，采用Galerkin法整理得
 （3）
将上式以矩阵形式表示并积分得：
 （4）
式中，[D]为总渗透矩阵，由单元渗透矩阵[D]叠加而成，[D]=∫[B][K][B]dA；[B]、[B]为形函数对坐标的微分向量， ；[K]为单元渗透矩阵；{h}为节点总水头列向量，{h}={h,h，…,h}；[E]为总贮水矩阵，由各单元贮水矩阵[E]叠加而成，[E]=∫[N]λ[N]dA， ；{F}为反映边界条件的流量矢量，{F}=∫NqdS。
对于时间的离散可以采用有限差分法。采用中心差分为：
 （5）
采用向后差分为：
  （6）
一般来说，中心差分法较向后差分法得到的结果精确；而向后差分法则在减小数值波动方面更为有效。
1.3有限元计算中几个问题的处理
2.3.1时间步的处理
在非稳定渗流计算中，时间步的取值不能过大，否则将不收敛或收敛太慢；时间步也不能太小，否则将产生过大的累积误差。在实际计算中，应先进行一定量的试算，根据计算的收敛情况选定一初始时间步进行计算。如果收敛，则取此值为该时段的步长，否则，时间步减半，直到获取收敛的时间步为止。
2.3.2入渗边界的处理
边界条件的确定是解决问题的关键之一。本文中采用的典型土坡剖面如图1所示，非饱和区边界AH、DE的状态很难确定。事实上，它是由上游和下游区域渗流情况确定的，具有不确定性，因此需要一定的假设，本文假设该区域不因降雨而和相邻区域发生水交换，即为不透水边界。
根据雨水入渗的实际特点，入渗边界可以考虑为两种模型：1）积水模型。当降雨强度小于土壤的入渗能力时，雨水将全部入渗，按第二类边界条件处理；2）降雨模型。当降雨强度超过土壤的入渗能力时，地表产生积水或径流，按第一类边界条件处理。本文根据初始条件和入渗过程的不同，将入渗边界AB、BC、CD按“积水模型”和“降雨模型”相互转化考虑，即按式（4）确定入渗能力q（t），在坡面法向上的分量为r（t）n，则入渗边界表示为：
当q（t）>r（t）n时，q（t）=r（t）n（7）
当q（t）r（t）n时，h（t）=h（t）（8）
式中，r（t）为降雨强度；n为边界面外法线方向余弦；h（t）为对应入渗边界的位置水头。
另外，假GF为不透水边界，EF、HG按固定水头边界考虑。当降雨总量保持不变，土坡的坡度由缓边陡后，入渗边界由积水模型向降雨模型转变。本文仅以边坡坡度1:1为例进行分析计算。
2算例
某均质土坡各相同性，不计变形对渗流的影响。坡高10m，坡度1:1，土坡剖面见图1。按降雨总量相同的条件，笔者考虑了9种降雨模型，以此来分析不同参数对基质吸力丧失量的影响，降雨模型见表1。降雨后，考虑到坡肩的孔隙水压力变化具有代表性，故仅以坡肩处（即图1中虚线BI）为例进行分析计算。
图1土坡剖面
Fig.1Slopeprofile
表1降雨模型
Table1Rainfallmodel
|
编号
|
降雨强度
r/（mm·h ）
|
降雨持时
t/h
|
饱和渗透系数
k /（m·s ）
|
|
No.1
|
60
|
8
|
10
|
|
No.2
|
60
|
8
|
10
|
|
No.3
|
60
|
8
|
10
|
|
No.4
|
30
|
16
|
10
|
|
No.5
|
30
|
16
|
10
|
|
No.6
|
30
|
16
|
10
|
|
No.7
|
15
|
32
|
10
|
|
No.8
|
15
|
32
|
10
|
|
No.9
|
15
|
32
|
10
|
3土坡稳定结果分析
3.1降雨强度与饱和渗透系数的影响
降雨强度与土壤饱和渗透系数是相互影响、相互制约的，需要将它们结合起来考虑。 1/2 1 2 下一页 尾页 |
