论文导读::基于无网格自然单元法,提出了结构动力弹塑性响应分析的一条新途径.自然单元法是一种新兴的无网格数值计算方法,其实质是基于自然邻近插值的伽辽金法.自然单元法在本质边界条件的施加上较采用移动最小二乘法的无网格法具有明显的优势.在空间域上采用自然单元法离散,并运用加权余量法推导了动力弹塑性分析的离散控制方程.然后,采用预校正形式的Newmark法在时间域上进行求解.最后给出了数值算例,并验证了所提方法的有效性和正确性.
论文关键词:无网格法,自然单元法,动力响应,弹塑性
0引言
在结构的动力响应过程中,通常总是既有弹性变形,又有塑性变形,而且这两种变形以及它们之间的分界面都随时间变化[1].正是由于弹塑性动力响应问题的复杂性,往往得不到结构弹塑性动力响应问题的解析解,需要借助数值方法进行求解. 在结构弹塑性动力响应的模拟方面,不论是有限元法[2]还是边界元法[3, 4],都是基于网格的数值方法.不合适的网格形状严重影响计算的精度,而且复杂结构的网格生成也是极具挑战性的问题. 相反,近年来发展迅速的无网格法具有近似函数不依赖于网格,且计算精度高,前后处理简单的优点[5].
目前发展的无网格方法主要有无单元Galerkin法[6, 7]、无网格局部Petrov-Galerkin法[ 8]、边界无单元法[9, 10]、杂交边界点法[11, 12]、无网格流形方法[13]以及自然单元法[14, 15]等. 与大多数无网格法不同,自然单元法的近似函数具有插值性且在边界结点间是线性变化的无网格法,从而可以方便地施加本质边界条件. 此外,自然单元法的形函数计算不仅具有不涉及矩阵求逆运算以及计算量较小的优点,而且也没有任何人为参数的选择问题. 因此,自然单元法是一种非常有发展前景的数值方法,并且已引起了国内外许多学者[16~22]的极大关注.
近年来,许多学者都致力于弹性动力学的无网格法研究. 程玉民等[10]将弹性动力学的边界积分方程方法与改进的移动最小二乘法结合,提出了弹性动力学的边界无单元法. 苗雨等[12]将双互易法同杂交边界点法相结合,提出了求解弹性动力学问题的双互易杂交边界点法. 李树忱等[13]运用无网格流形方法求解了弹性动力学问题. 刘应华等[23]发展了弹性动力学分析的基于Voronoi结构的无网格局部Petrov-Galerkin法. 虽然朱合华等[19],张英新等[20]和江涛等[21]在无网格自然单元法应用于弹塑性力学问题方面做了一些有益的工作,但目前尚未见到动力弹塑性分析中无网格自然单元法的研究成果.
本文尝试将自然单元法应用于动力弹塑性分析问题的求解计算. 首先采用加权残值法详细推导了动力弹塑性分析的自然单元法理论公式,然后给出了其详细的数值实现过程. 最后,通过典型算例的计算和对比分析验证了方法的有效性和合理性.
1 控制方程
考虑二维动力弹塑性分析问题,其计算域为 ,边界为 ,边界为 ,则平衡方程为: ,则平衡方程为:
 (1) (1)
式中, 为质量密度; 为质量密度; 为结点加速度,且有 为结点加速度,且有 , , 为结点位移; 为结点位移; 为应力; 为应力; 为应变; 为应变; 为体力矢量; 为体力矢量; 和 和 分别为位移和面力已知的边界. 分别为位移和面力已知的边界.
应力和位移满足如下的边界条件
 (2a) (2a)
 (2b) (2b)
和初始条件
 (3a) (3a)
 (3b) (3b)
式中, 为 为 上点 上点 处的外法线的方向余弦; 处的外法线的方向余弦; 和 和 分别为已知的位移和面力分量; 分别为已知的位移和面力分量; 和 和 分别为初始位移和初始速度. 分别为初始位移和初始速度.
弹塑性材料在进入塑性状态后,继续加载时的应力应变关系可以表示为
 (4) (4)
式中, 为总应变增量. 采用关联的流动法则以及各向同性的加工强化模型,可得到弹塑性刚度张量为[ 2] 为总应变增量. 采用关联的流动法则以及各向同性的加工强化模型,可得到弹塑性刚度张量为[ 2]
 (5) (5)
其中
 (6a) (6a)
 (6b) (6b)
 (6c) (6c)
这里, 和 和 分别为等效应力和等效塑性应变, 分别为等效应力和等效塑性应变, 为单向屈服应力,而 为单向屈服应力,而 和 和 分别为剪切模量和泊松比. 分别为剪切模量和泊松比.
2 动力弹塑性分析的无网格自然单元法
2.1 自然邻近插值[14~23]
自然邻近插值是一种多变量的插值方案,目前应用于无网格法的有Sibson插值和Laplace插值.本文采用Sibson插值.
对区域 内任一结点 内任一结点 ,其Voronoi结构定义为: ,其Voronoi结构定义为:
 (7) (7)
式中, 为点 为点 与结点 与结点 的距离.此外无网格法,二次Voronoi结构 的距离.此外无网格法,二次Voronoi结构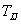 可定义为: 可定义为:
 (8) (8)
图1所示为平面7个结点的Voronoi结构和待插值点 的二次Voronoi结构. 的二次Voronoi结构.
对于Sibson插值,计算点 对结点 对结点 的形函数 的形函数 定义为 定义为 与结点 与结点 的二次Voronoi结构 的二次Voronoi结构 的面积 的面积 与 与 的一次Voronoi结构 的一次Voronoi结构 的面积 的面积 之比,即 之比,即
1/3 1 2 3 下一页 尾页 |


