 (9) (9)
定义了各结点的插值函数后,点 的位移函数类似于有限元法可写为 的位移函数类似于有限元法可写为
 (10) (10)
式中, 是点 是点 周围自然邻结点 周围自然邻结点 的结点位移, 的结点位移, 为对应结点的形函数. 为对应结点的形函数.
2.2 控制方程的弱形式及其离散化
平衡方程式(1)及力的边界条件式(2b)的等效积分形式的伽辽金提法可以表示为
 (11) (11)
对式(11)进行分部积分,则有
 (12) (12)
为便于进行数值计算,我们把上式改写成矩阵形式,有
 (13) (13)
式中
 (14) (14)
由于只对空间域进行离散,求解域 内的试函数 内的试函数 可由式(10)表示为 可由式(10)表示为
 (15) (15)
将空间离散后的位移表达式(15)代入式(14),并注意到结点位移变化 的任意性,最终得到系统的运动方程如下: 的任意性,最终得到系统的运动方程如下:
 (16) (16)
式中, 为结点的加速度向量; 为结点的加速度向量; , , 和 和 分别为质量矩阵、结点内力向量和结点外力向量,且它们各元素可具体表示为: 分别为质量矩阵、结点内力向量和结点外力向量,且它们各元素可具体表示为:
 (17a) (17a)
 (17b) (17b)
 (17c) (17c)
其中
 , ,  (18) (18)
3 时间积分方案
本文对时间域的离散采用应用较为广泛的Newmark方法[2].Newmark 方法是一种隐式算法,因此时刻 的运动方程应得到满足.此外,由于塑性变形的非线性特性,在每个时间步都必须进行迭代计算.应用Newton-Raphson迭代,时刻 的运动方程应得到满足.此外,由于塑性变形的非线性特性,在每个时间步都必须进行迭代计算.应用Newton-Raphson迭代,时刻 的运动方程可以改写为 的运动方程可以改写为
 (19a) (19a)
 (19b) (19b)
式中,切线刚度矩阵 可以表示为 可以表示为
 (20) (20)
在 和 和 时间步内,Newmark方法采用的位移和速度的递归关系为 时间步内,Newmark方法采用的位移和速度的递归关系为
 (21a) (21a)
 (21b) (21b)
其中 和 和 是按积分精度和稳定性要求决定的参数. 由式(19b)和式(21b)可得 是按积分精度和稳定性要求决定的参数. 由式(19b)和式(21b)可得
 (22) (22)
将式(22)代人式(19a),则得到如下的静力等效问题
 (23) (23)
式中
 (24a) (24a)
 (24b) (24b)
顺便指出,给定初始的位移 和初始速度 和初始速度 后,我们就可以从下式求出初始加速度 后,我们就可以从下式求出初始加速度 : :
 (25) (25)
下面给出 时刻静力等效问题(23)的具体迭代求解过程: 时刻静力等效问题(23)的具体迭代求解过程:
(1)令迭代计算变量 . .
(2)在开始预估阶段,令
 (26a) (26a)
 (26b) (26b)
 (26c) (26c)
式中
 (27) (27)
(3)利用下述方程计算残余力
 (28) (28)
(4)如有需要,应用下式形成等效刚度矩阵
 (29) (29)
否则,就应用前面已计算出的 . .
(5)求解方程
 (30) (30)
得到结点位移增量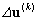 ,然后利用几何关系可计算得到应变增量 ,然后利用几何关系可计算得到应变增量 .在此基础上,利用第1节中所述的弹塑性本构关系以及切向预测径向返回方法[24]就可以确定应力 .在此基础上,利用第1节中所述的弹塑性本构关系以及切向预测径向返回方法[24]就可以确定应力 . .
(6)进入修正阶段无网格法,令
 (31a) (31a)
 (31b) (31b)
 (31c) (31c)
(7)如果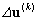 不满足收敛条件,令 不满足收敛条件,令 并转到第3步,否则继续进行下去. 并转到第3步,否则继续进行下去.
(8)为下一个时间步使用,令
 (32a) (32a)
 (32b) (32b)
 (32c) (32c)
2/3 首页 上一页 1 2 3 下一页 尾页 |


