结构6：中间产品市场分工结构a，此时用中间产品 或 进行生产x，最后形成了x与的市场，一部分人买或卖x，另一部分人买x卖或，最终均衡解为：
 ，
 ；
结构7：中间产品市场分工结构, 此时用中间产品和生产x，形成了、和x的市场，最终形成的均衡解为：
 ，
 ；
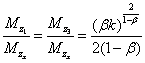
产品y的均衡角点解与x的相同，只是因为本文假定各个市场的交易效率相同的缘故。
用 便得到生产性服务业由于横向分工所得到的发展，于是
 （15）
于是，根据上文讲过的思路，本文将由于横向和纵向分工所导致的生产性服务业的发展进行加总。最后，讲（3-1-8）和（3-2-7）相加毕业论文的格式，便可以得到生产服务业的发展模型：
 （16）
公式（16）表明，生产性服务业的发展的内生机制包括交易效率（ ）、中间产品种类数（ ）、迂回生产程度（b）、专业化程度（ ）、创新动力水平（ ），各变量均与生产性服务业的发展呈现出正相关的关系。迂回生产程度（b）、专业化程度（）对于生产性服务业的发展比较复杂，这涉及到了横向分工和纵向分工的综合效应，其效应可正可负，取决于有多样化和迂回生产程度引起的交易效率的提高是否可以抵消来自相关方面的成本。由于本文论述了专业化水平由时间（t）决定，交易效率包括最终产品（ ）和中间（生产性服务业）产品市场的交易效率（ ），创新动力水平由城市化水平决定，再加上迂回生产程度和中间产品种类数。最终，本文得出的生产性服务业的发展模型为：
 （17）
四 实证检验
前文利用分工理论构建了关于生产性服务业的发展模型，下来便可以对我国的生产性服务业的发展进行区域差异的分析。比较各种方法后本文最终选取了夏普里值（Shapley value）的分解方法以及其需要的关于生产性服务业的发展模型。
（一）变量选取和数据来源
1.生产性服务业指标：对于生产性服务业的指标，本文选取了交通运输及仓储和邮电业、金融业、教育及科学研究行业[⑤]这几个指标用的人均产出进行衡量；
2.交易效率：根据上述分析，本文得出了最终产品和中间产品市场的交易效率对于生产性服务业的正向关系。于是，本文选取了制造业的交易效率来替代最终产品市场上的交易效率，交通、教育、金融、信息市场上的交易效率来体现中间产品市场上的交易效率，具体核算方法如下：
（1）制造业的交易效率：在核算其交易效率之前，首先需要得出制造业的统计指标。限于数据来源，本文最终选取了第二产业的产出增长率来进行衡量，在对产出增长率进行无量钢化最终得出最终产品市场的交易效率；
（2）交通交易效率：根据高帆（2007），本文选取了每万人的人均铁路、公路和航运里程数，然后进行无量钢化，最后用三种交通方式的货物额占总额的比重进行加权，最终得到了商品市场的交易效率；
（3）信息交易效率：本文选取了每万人的人均固定电话、移动电话、国际互联网进行无量钢化，在进行简单平均，得出信息交易效率；
（4）金融市场的交易效率：考虑到数据的来源性，本文选取了金融、保险业的产值占GDP的比重加以反映，然后进行无量钢化，最终得出金融市场的交易效率；
（5）教育市场的交易效率：本文利用公共财政在教育、科学研究行业上的支出占总支出的比重进行衡量，然后再进行无量钢化，得出教育市场的交易效率。
3.专业化程度指数：根据李敬（2007）的做法，本文用时间虚拟变量来作为对于专业化程度的替代；
4.创新动力指数：本文认为其由城市化水平决定，城市化水平由城镇就业总人口占总就业人口的比重来进行衡量；
5.差异指标：本文利用生产性服务业的产值水平最终核算了该行业的基尼（gini0）、对数离差均值（gini1）和泰尔（theil）指标。
由于无法对中间产品种类数和迂回生产程度进行量化，本文最终放弃了这两个变量，最终得出的面板模型为：
 （18）
公式（18）中， 为反映专业化程度的时间虚拟变量， 、 、 、 、 分别代表制造业、交通、信息、金融和教育市场的交易效率， 为反映城市化水平的自然对数值， 为共同截距项， 为界面虚拟变量， 为误差项。
本文所使用面板数据的时间跨度为2001-2007年，地域为全国除港澳台的31个省区，划分以统计年鉴上的区分为准。数据来源于各年的统计年鉴、中国劳动统计年鉴。对于人均GDP，本文采用实际指标毕业论文的格式，具体计算方法是以2001年为基期，换算出定基的价格指数，然后在人均GDP中剔除价格水平。
（二）生产性服务业面板协整模型
1．各变量的单位根检验
为了避免虚假回归，首先对各变量变量进行单位根检验。面板模型中包含有四种检验方法，分别是Levin，Linand Chu检验(2002)、Im Pesaran and Shin W检验(2003)、ADF-Fisher Chi-square检验（1999）和PP-Fisher Chi-square检验（2001）。这四种方法互相补充，一般认为，四种检验均通过时，可认为是平稳性数据，滞后期数根据AIC原则进行选取。检验结果如下所示：
表1：内生机制各变量单位根检验
|
变量
|
Levin，Lin&Chu
|
Im，Pesaran and Shin W-stat
|
ADF-Fisher Chi-square
|
PP-Fisher Chi-square
|
|
LNPSI
D（LNPS）
lncity
D（lncity）
k1
D（k1）
k2
D（k2）
k3
D(k3)
k4
D(k4)
K5
D(k5)
|
-2.69381***
-9.25938***
0.12233
-22.6365***
--1.2041*
-20.0640***
-51.2041***
-20.0640***
-65.4170***
-138.560***
-1.74452***
-2.74452**
-7.23769***
-8.90421***
|
5.22818
-1.59713*
2.44486
-7.87601***
-4.36611***
-5.18634***
-7.87601
-5.18634***
-35.0316*
-59.6542***
0.84426
-25.845628*
-0.79098
-2.67742***
|
42.6745
82.9673***
57.5026
174.332***
53.5887
130.597***
53.5887
130.597***
24.762
397.374**
49.7794
74.0232**
80.9438*
105.4612***
|
12.1049
102.576***
59.5385*
190.222***
29.0161
151.026***
29.0161
151.026***
32.842
445.892***
42.6717
79.2008**
69.8589
120.372***
|
注：结果由EViews5.0计算得出
*、**、***分别表示统计值在10%、5%和1%的水平上显著。
检验结果显示LNPS、lncity、k1、k2、k3、k4、k5、在未进行差分时统计值均大于临界值，均不能在显著性水平为5%的水平上拒绝有单位根的假设，属于非平稳序列，而在进行一阶差分后各变量的统计值均小于临界值，差分平稳，属于1阶单整序列，可以进行协整检验。
2．协整检验
单位根检验结果显示各统计指标1阶单整序列，可以对各变量进行协整测试论文开题报告范例。具体方法是先对各变量进行回归分析，然后对得到的残差序列进行单位根检验，如残差序列统计值小于临界值，则说明各变量存在着协整关系。进行回归分析时，本文利用F检验、Hausman检验和Redundant Fixed Effects检验选取了基于截面和时间固定效应的变截距模型，估计的具体方法是以估计截面残差方差的残差为权数的cross section weights。模型的回归结果如下：
3/4 首页 上一页 1 2 3 4 下一页 尾页 |
