。 用基金收益率减去同期无风险收益率再除以基金收益率的标准差就能得到,该指标目前已经成为国际通用的衡量基金业绩的核心指标。 用基金收益率减去同期无风险收益率再除以基金收益率的标准差就能得到,该指标目前已经成为国际通用的衡量基金业绩的核心指标。
贝塔值 。理论上,理性投资者在投资风险资产时除了考虑收益外还要考虑风险。 。理论上,理性投资者在投资风险资产时除了考虑收益外还要考虑风险。 衡量了基金的系统风险。 衡量了基金的系统风险。
总体风险 。基金的风险不仅包括系统风险,还包括个体风险。由于我们的样本为普通股票型开放式基金,基金管理人可以根据自己的预期选择与指数有较大差异的投资组合,使得个体风险增加,因此基金总体风险与系统风险会存在较大差异。 。基金的风险不仅包括系统风险,还包括个体风险。由于我们的样本为普通股票型开放式基金,基金管理人可以根据自己的预期选择与指数有较大差异的投资组合,使得个体风险增加,因此基金总体风险与系统风险会存在较大差异。
(二)方法
一般认为,基金的赎回率主要受到基金业绩的影响,而这种影响并非是同质的,基金业绩可能会对不同的基金赎回率产生不同的影响,因此需要分析基金业绩对基金赎回率条件分布形状的影响,但是传统的以最小二乘法为基础的统计方法只能描述自变量对因变量条件均值的影响,所以本文采用分位数回归方法检验“赎回之谜”。
分位数回归方法最早由KoenkerandBassett(1978)提出,与最小二乘法描述自变量对应变量条件分布均值的影响不同,分位数回归刻画了自变量对因变量条件分布不同分位数的影响,而且不易受到数据非正态性的影响,因此,与最小二乘法相比分位数回归更加稳健且能刻画因变量条件分布的形状。
当前面板数据分位数回归方法均假设个体效应为固定效应,从而得到如下模型:
 (2) (2)
其中, 为给定 为给定 条件下 条件下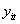 的 的 分位数。 分位数。
三、实证检验
我们首先对各变量进行了描述性统计,分析结果见表1。
接下来,我们建立如下面板数据模型进行分析,分析结果见表2。
 (3) (3)
其中, 表示截面, 表示截面, 表示时间, 表示时间, 表示截面 表示截面 的个体效应, 的个体效应, 代表基金收益率, 代表基金收益率, 代表夏普比率, 代表夏普比率, 代表贝塔值, 代表贝塔值, 代表总体风险。 代表总体风险。
表1变量描述性统计表
|
|
净申购率
|
基金收益率
|
夏普比率
|
贝塔值
|
总体风险
|
|
均值
|
0.4524
|
5.8126
|
0.0575
|
0.7602
|
0.0558
|
|
中位数
|
-0.0311
|
1.8579
|
0.0032
|
0.7566
|
0.0561
|
|
标准差
|
1.9629
|
19.2912
|
0.1673
|
0.1152
|
0.0131
|
|
最大值
|
18.7788
|
46.0077
|
0.3709
|
1.1371
|
0.0930
|
|
最小值
|
-0.5809
|
-30.4140
|
-0.2470
|
0.4228
|
0.0276
|
|
样本数
|
416
|
416
|
416
|
416
|
416
|
|
J-B(p-值)
|
0.0000
|
0.0000
|
0.0000
|
0.8731
|
0.3584
|
从表2中我们可以看到,无论是在随机效应模型还是在固定效应模型中,基金收益率与基金净申购率都是显著正相关的,这与束景虹(2005)的结论一致。但是如果用夏普比率衡量基金业绩的话,基金业绩与基金净申购率负相关但不显著。基金系统风险与基金净申购率显著负相关,与基金总体风险显著正相关。由于数据的非正态性会影响估计的效果,而且为了更深入的考察“赎回之谜”的存在性及其条件和范围,我们下面采用面板数据分位数回归方法进行检验,Hausman检验的p值为0.0877,在10%的置信水平下支持固定效应的假设。
我们依照(2)式建立固定效应下的面板数据分位数回归模型,其中解释变量 包括 包括 、 、 、 、 、 、 和常数项。为了能够更加全面的考察解释变量对被解释变量条件分布的影响,本文选择几个代表性的分位点。回归结果见表3。 和常数项。为了能够更加全面的考察解释变量对被解释变量条件分布的影响,本文选择几个代表性的分位点。回归结果见表3。
表2面板数据模型分析结果
|
|

|

|
|

|
-0.07837 (-0.1173)
|
0.9751 (1.0893)
|
|

|
0.0600 (2.5775)
|
0.0651 (2.7469)
|
|

|
-3.0249 (-1.1205)
|
-3.5214 (-1.2812)
|
|

|
-1.8260 (-2.0833)
|
-3.0462 (-2.7846)
|
|

|
31.2579 (3.8632)
|
28.9968 (3.4820)
|
|

|
0.1054
|
0.1486
|
|
F
|
12.0997
|
1.8948
|
|
FE or RE
|
RE
|
FE
|
|
Hausman
|
8.1070
|
|
Prob(Hausman)
|
0.0877
|
注:括号里面的为相应回归系数的t值;表示在5%的显著性水平下显著;表示在1%的显著性水平下显著。
我们首先分析净申购率与基金收益率的关系。结果显示,基金收益率对净申购率的影响是非对称的。处于低分位点位置的净申购率与基金收益率负相关,符合“赎回之谜”之谜假说,这与陆蓉等(2007)的研究结论一致。随着净申购率分位点的提高基金收益率的影响变得不显著,随着分为点的进一步提高基金收益率的影响由负转正,并且影响强度不断提高,不支持“赎回之谜”假说,这与束景虹(2005)的研究结论一致。由此我们认为,当基金业绩用基金收益率衡量时,基金业绩对净申购率的影响是非对称的,“赎回之谜”发生在净申购率的低分位点部分(即净赎回率的高分位点部分),而大于80%的情况下并未表现出“赎回之谜”,并且对特定部分的净申购率基金收益率的影响不显著(见图2)。我们认为这一现象的原因是“认知失调”,当新发生的事件与原有的认识发生不一致时,个人会产生沮丧。为了避免“认知失调”带来的痛苦,基金表现良好时,投资者会积极买入,但基金表现较差时,投资者却不愿卖出。
表3固定效应面板数据分位数回归结果
|
解释
变量
|
分位点及回归结果
|
|
t=0.125
|
t=0.200
|
t=0.250
|
t=0.375
|
t=0.500
|
t=0.625
|
t=0.750
|
t=0.875
|
|

|
-0.2092
(-1.4111)
|
-0.2186
(-1.5263)
|
-0.0845
(-0.6614)
|
-0.1297
(-1.1248)
|
-0.1718
(-1.8309)
|
-0.1653
(-1.2406)
|
0.0602
(0.0700)
|
0.9307
(0.5245)
|
|

|
-0.0034
(0.0122)
|
-0.0017
(-0.9168)
|
-0.0005
(0.8035)
|
0.0032
(0.1364)
|
0.0058
(0.0857)
|
0.0363
(0.0333)
|
0.0318
(0.0112)
|
0.1184
(0.0010)
|
|

|
0.1193
(0.8931)
|
0.0651
(0.4179)
|
-0.0075
(-0.0433)
|
-0.2269
(-1.1834)
|
-0.4530
(-1.5006)
|
-0.9496
(-1.9824)
|
-2.3819
(-2.3599)
|
-8.5137
(-2.9637)
|
|

|
-0.0970
(-1.2988)
|
-0.0547
(-0.6989)
|
-0.0758
(-0.9395)
|
-0.0915
(-1.2809)
|
-0.0332
(-0.3747)
|
-0.1171
(-0.8358)
|
-0.5728
(-1.4071)
|
-2.6927
(-2.3035)
|
|

|
-1.1599
(-2.0430)
|
-0.3992
(-0.6318)
|
0.0334
(0.0513)
|
1.1639
(1.6869)
|
1.9650
(2.2209)
|
10.4805
(2.3159)
|
8.2737
(2.6081)
|
33.9085
(3.4247)
|
|
伪
|
0.0822
|
0.0423
|
0.0299
|
0.0200
|
0.0169
|
0.0237
|
0.0507
|
0.1590
|
|
拟LR
|
127.8855
|
84.4039
|
74.5048
|
61.7889
|
61.0994
|
78.0491
|
118.9940
|
122.8540
|
|
Prob
(拟LR)
|
0.0000
|
0.0000
|
0.0001
|
0.0035
|
0.0041
|
0.0000
|
0.0000
|
0.0000
|
注:括号内为相应的t值,表示在10%的显著性水平下显著,表示在5%的显著性水平下显著,表示在1%的显著性水平下显著。
然后我们分析净申购率与夏普比率的关系。夏普比率对净申购率的影响同样是非对称的,夏普比率对较低部分的净申购率影响不显著,对较高部分净申购率的影响显著为负。因此,如果用夏普比率作为基金业绩衡量指标的话,基金业绩对大于50%情况下的净申购率无显著影响;对一定分位数以上的净申购率的影响为负,表现出“赎回之谜”(见图3)。这反映出我国开放式基金投资者目前尚处于不成熟状态,作为公认基金业绩衡量指标的夏普比率没有成为投资者挑选基金的标准,这反而会对基金管理人的行为造成扭曲。
为了检验结果的稳健性,我们还把由贝塔值 和总体风险 和总体风险 构成的控制变量的不同组合情况进行了检验,结论无实质性改变。 构成的控制变量的不同组合情况进行了检验,结论无实质性改变。 2/3 首页 上一页 1 2 3 下一页 尾页 |


