论文导读:：近年来，随着祖国大陆和台湾的经济、金融交流越来越深入和频繁，反映国民经济运行状况的两岸股市呈现出越来越明显的共同运动的趋势。本文运用Johansen协整检验、格兰杰因果检验，脉冲响应函数、方差分解对沪深300指数与台湾加权指数的关联性进行检验和分析。实证结果表明，沪深300指数与台湾加权指数之间存在显著的协整关系；格兰杰因果检验发现，沪深300指数对台湾加权指数有一定的引导作用；最后应用脉冲响应和方差分解的实证方法从另一角度证实了上述结论。
论文关键词：沪深300指数，台湾加权指数，协整，格兰杰因果检验，脉冲响应，方差分解
一、引言
随着全球经济一体化趋势进程的加快，世界经济的趋同现象已在证券市场上有所表现，各地证券市场的相互影响日益扩大，国际股票市场的联动性增强。因此，股票指数间的研究备受关注，国内外不少学者做了相关研究。
Jeon和Furstenberg(1990)认为，国际证券市场各主要股票市场指数呈现出越来越明显的共同运动趋势。陈守东、韩广哲等（2003）证实了1992年11月20日至2002年7月12日间，世界主要股票市场（美国、英国、香港、日本）之间存在显著的协整关系，国内沪、深两市指数间也存在显著的协整关系，但我国股票市场与世界主要股票市场之间不存在协整关系，得出我国股票市场与国际市场相分离的结论。高莹（2008）发现随着我国经济的发展，证券市场与美英等主要经济国家的交流与联系日益密切，2005年1月4日至2006年12月19日，沪深300指数与除日经指数外的其它世界主要指数存在长期协整关系，世界主要市场股票指数对沪深300指数有较强的引导作用。张福、赵华（2004）选取1996年到2002年上证指数和美国S&P500指数为研究对象，并以2001年2月19日为界来分析中美股市协整关系，结果表明在2001年以前两股市间不存在协整关系，而2001年以后中美股市间存在协整关系。吴世农、潘越（2005）发现红筹股、H股和内地股市之间存在长期稳定的协整关系，这一均衡关系在B股开放后进一步加强，并且红筹股的走势始终是内地股市的“风向标”。史代敏（2002）用1993年1月1日至2001年7月31日的数据样本证实上证指数与深圳综合指数之间存在协整关系，表明沪深两市间存在长期稳定的联动关系。
由上可见，中国股市与世界几个重要股市的关系备受关注；由于香港在全球经济与金融的显赫地位，学者对大陆股市与香港股市的关系也做了相关研究；在大陆股市内部，关于沪市和深市，及A股和B股等之间的联动性的研究也有很多。长期以来，由于政治与制度等因素的原因，大陆与台湾两岸经贸金融合作有限，台湾股市与大陆股市的联动程度很低，大陆股市的波动对台股几乎没有影响。因此，很少有文献对两岸股市关系进行讨论。但近年来，随着大陆经济发展、两岸经贸关系的日益密切，台湾经济受大陆经济影响力的增强，台湾股市行情受到大陆经济与股市的影响越来越明显。
本文应用2003年度诺贝尔经济学奖获得者Engel和Grange提出的“协整关系检验”和“因果关系检验”，来分析沪深300指数和台湾加权指数协整关系和引导关系。最后用脉冲响应函数、方差分解从另一个角度再次验证了两指数的引导关系。
二、数据选择及处理
考虑到数据的完整性和代表性，本文选取了沪深300指数（HS300）和台湾加权指数（TWII）分别作为作为大陆股市和台湾股市的代表。之所以选择沪深300，而没选用通常所用的上综指，是因为沪深300指数涵盖了沪深两市股票，能够真实反映中国A股市场的股价综合走台走势方差分解，更全面。沪深300指数数据来自国泰安经济研究数据库，台湾加权数据来自雅虎财经网。时间跨度为2008年1月2日至2010年7月2日，所采用的样本为各指数的日收盘数据。
由于大陆与台湾股市开市休市并不一致，如节假日等都会令两地股指在时间上不能匹配，为了保证两个价格时间序列样本的一致性，剔除了有股指没有交易的那些日期的数据。经处理，共得到594个数据。
另外，按照惯例对股价序列进行对数化处理，使其平稳化。两个对数化股价序列分别记做LNLHS300,LNLTWII。分析软件采用EViews6.0.
三、模型简介
1、单位根过程
如果非平稳时间序列 经过 次差分后变为平稳时间序列，则称该序列为 阶单整序列，记为 。其中表示单整阶数，是序列包含的单位根个数。
序列是 而不是 的检验被称作单位根检验。标准的单位根检验方法是DF检验。这一过程中没有考虑残差的自相关，故解决这个问题的一种方法是加入因变量的多阶滞后项来消除残差自相关，这就是ADF（augment Dickey-Fuller）检验。其回归方程式为：
 
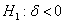
将所求出的ADF的t统计量与临界量 相比，若 ，那么存在单位根的零假设被拒绝，认为序列是平稳的；反之，没有充分理由拒绝零假设，原序列存在单位根，为非平稳序列。
2、协整
长期以来，人们发现许多经济时间序列都呈现出明显的非稳定的单位根过程的特征，若直接对这些序列之间的关系作分析，正如菲利普斯从理论上所证明的：不相关的单位根变量之间会产生“伪回归”现象，从而导出不正确的结论。但是如果只是对一阶差分之间的关系作分析，则可能丢掉原序列的有效信息，协整理论有效的解决了这一问题。
若时间序列 都是d阶单整序列，且存在一个向量 ，使得 ，其中 。那么称序列是 (d, b) 阶协整，记为 ， 为协整向量。
协整性检验的方法有基于回归残差的EG(Gngel-Granger,1987)两步法和基于回归系数的Johansen(Jonhsen-Juselius,1990)协整检验。本文采用后者进行分析。
Johansen协整检验方法是在VAR模型中利用极大似然估计来检验多个变量间的协整关系的方法。假设 和 分别是k阶和d阶的向量，均服从I（1）过程，先建立如下的VAR模型：
其中：
Johansen证明，系数矩阵 包含了变量之间长期均衡关系的信息----协整向量。如果系数矩阵的秩 ，则存在 阶矩阵和 ，使得，其中是调整参数矩阵，是由 个相互独立的协整列向量组成的矩阵，即 服从 过程。令 ，矩阵的秩等于 的独立协整向量的个数。Johansen证明可以通过检验矩阵的特征根的显著性，确定出协整向量的个数。
1/3 1 2 3 下一页 尾页 |
