产业聚集与区域经济增长的关系研究——以西部十省的实证分析为例-论文网

1．经济活动密度

一个地区经济活动密度是用每平方公里的就业数量来衡量，因为就业数量可以在一定程度上反映出某个地区经济发展的水平，因此经济活动密度可以间接的检验增长和聚集的关系。通过计算经济活动密度并从高到低的顺序对西部十省进行了排序，并与全国水平进行了比较（见表1）。与全国相比西部十省的经济活动密度明显偏低，排除西部地区面积较大，人口稀少的因素，我们认为主要是不合理的产业结构引起的，同时，要素流动性偏弱也是重要的制约因素之一。

表1.2008年西部十省经济活动密度

2．三次产业区位基尼系数

洛仑兹曲线和基尼系数用来衡量收入、消费和财富的不平等。如果将传统的洛伦兹曲线和基尼系数的人口用区位变量替代，收入用产业变量替代时，就形成了产业区位洛伦兹曲线和区位基尼系数，它反映产业活动在地区间的分配均衡程度。产业区位洛伦兹曲线弯曲程度越大，基尼系数越接近1，经济活动的空间分布越集中。因此本文通过数据的处理然后画出西部十省的产业区位洛伦兹曲线，然后通过洛伦兹曲线计算产业区位基尼系数（见图1）。通过图形的变化可以看出，从改革开放到现在，西部十省三次产业的基尼系数并未出现大的波动。相对而言，第一产业的区位基尼系数从改革开放以来呈现明显的下降趋势，然后进入一个相对平稳期，可以推测随着农业生产技术的推广，由地理因素引起的农业生产条件差异正在逐渐消失。第二产业区位基尼系数从改革开放开始进入一个相对平稳期，而到了上世纪90年代后期，特别是西部大开发战略实施后出现一个小的波动期，出现了先上升后下降在上升的过程，可以推断政策调控对第二产业的影响较大。第三产业的区位基尼系数变化较大，而且不存在很明显的规律性，我们认为第三产业由于在发展过程中受到资源和区位等的影响因素较少，出现某一区域的跨越式发展是出现这一现象的主要原因。

图1.1978-2008年西部十省三次产业区位基尼系数变化图

（二）经济增长的动态变化

西部地区名义人均GDP的增长率变化幅度较大，尤其是在是从1994-1999年增长率呈现下降趋势，但是随着西部大开发的不断深入，增长率稳步提高，可以看出西部大开发对西部地区经济发展的影响之大。但是更为重要的是我们发现西部地区经济增长没有明显的趋势性，我们推断不完善的市场制度使得西部地经济发展呈现明显的政策依赖性，随着国家政策的调整，经济增长速度呈现出一定程度的相应变化。（见图2）。

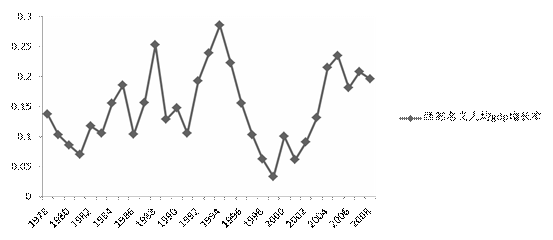
图2.西部地区1978-2008年名义人均GDP增长率

（三）经济增长与产业聚集

西部名义人均GDP的变化幅度明显大于三次产业区位基尼系数的变化幅度，而且直观上看变化趋势之间并不存在明显的同步性，经济增长速度的大幅度变化并未引起产业结构剧烈的变化，同时相对稳定的产业结构也没能带来经济稳定快速的增长（见图3）。本部分只是通过统计描述对西部十省经济增长的情况和三次产业聚集态势的变化以及两者的关系进行了初步分析，并对原因进行了尝试性推断。下面将通过计量方法，对两者之间的关系进行更加深入的研究。

图3.人均GDP增长率与三次产业区位基尼系数关系图

四．实证分析及结论

（一）宏观生产模型的引入与扩展

柯布-道格拉斯生产函数是由数学家柯布和经济学家道格拉斯于20世纪30年代初一起提出来的，是预测国家和地区的工业系统或大企业的生产和分析发展生产的途径的一种经济数学模型，简称生产函数，它的基本的形式为：

（1）

式中Y是工业总产值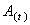，是综合技术水平，K是投入的资本要素，一般指固定资产净值，L是投入的劳动力人数，α是资本产出的弹性系数，β是劳动力产出的弹性系数，μ表示随机干扰的影响，μ≤1。在此基础上我们得到基本的宏观生产函数，其对数形式如下：

（2）

其中，Y代表GDP，K是以全社会固定资产投资为衡量标准的要素投入，L为全社会从业人数为代表的劳动力要素投入，C是常数项，ε是残差项。

为了验证三次产业聚集态势，我们引入第一产业区位基尼系数、第二产业区位基尼系数、第三产业区位基尼系数对宏观生产函数（2）进行谨慎扩展，同时由于我们主要是为了验证产业聚集与经济增长的关系，因此我们将方程中的有些变量进行处理得到名义GDP的人均增长率，社会固定资产投资增长率，从业人数在总人口中的比重三个指标，分别用，，表示，得到本文验证所用的方程，其形式如下：

（3）

（二）协整检验

1．单位根检验

为了保证检验结果的稳定性，我们首先采用ADF检验对方程中涉及的六个时间序列变量做了单位根检验。从检验结果来看：有些序列包含了确定的时间趋势，但是这些序列中含有单位根，也就是说时间序列中含有随即游走的成分；而当采取一阶差分的方式对序列进行检验时，统计结果拒绝了具有单位根的原假设。

 2/4   首页 上一页 1 2 3 4 下一页 尾页