现在对应分析完全竞争市场条件下的政府投资决策。假设 是时期 是时期 状态 状态 下的投资净收益,于是有 下的投资净收益,于是有 才会进行投资,这等价于 才会进行投资,这等价于 。假设投资净收益独立于先前的投资,独立于个体的效用函数,并且有一个客观的概率分布,且各种状态是相互独立的。将所有自然状态可以分割为相互没有交集,相互独立的状态集合 。假设投资净收益独立于先前的投资,独立于个体的效用函数,并且有一个客观的概率分布,且各种状态是相互独立的。将所有自然状态可以分割为相互没有交集,相互独立的状态集合 ,且对于任意个体 ,且对于任意个体 ,当 ,当 ,其效用函数 ,其效用函数 ( (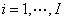 )相同。同时也可以将所有自然状态分割为相互没有交集,相互独立的状态集合 )相同。同时也可以将所有自然状态分割为相互没有交集,相互独立的状态集合 。对 。对 , , 是相同的。假设 是相同的。假设 ( ( ),当 ),当 , , 。令 。令 ,即表示上述两集合中所有自然状态的集合。将先前讨论中的状态 ,即表示上述两集合中所有自然状态的集合。将先前讨论中的状态 用 用 代替,则有 代替,则有 ,由前述假设可知 ,由前述假设可知 。又由(2)式可得 。又由(2)式可得 。令 。令 ,可以认为是任意个体在状态 ,可以认为是任意个体在状态 时期 时期 的单位货币商品边际效用,则有 的单位货币商品边际效用,则有 。 。
由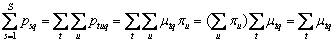 ,可知时期 ,可知时期 , , 状态集合中的单位商品价格现值和与所属个体无关,并且等于该状态集合中时期 状态集合中的单位商品价格现值和与所属个体无关,并且等于该状态集合中时期 的单位货币商品边际效用和。又因为 的单位货币商品边际效用和。又因为 , , 相同,所以 相同,所以
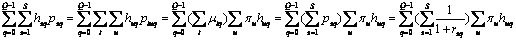 (3) (3)
(3)式表明满足独立条件的投资净收益现值和等于每期净收益预期值的现值和,并且与个体无关。这是在完全竞争条件下无需考虑风险调整情况下的政府投资决策。
(二)、不完全竞争条件下的政府投资决策分析
现实中由于道德风险和高额交易成本等存在,使得完全竞争的条件并不满足,所以上述分析结果是次优的。当不完全竞争时,政府应该如何对待投资决策中的不确定性?下面在假设个体偏好同政府投资决策有关的基础上,分析了此问题。
假设个人效用仅依赖于消费,而不依赖于消费发生的状态。在该假设下,时间因素和风险偏好相分离,只需分析单个时期的情况。假设政府投资支出源于个体纳税人,且共有 个纳税人,政府投资净收益由纳税人平均分享。一般个体均是风险规避的,并设个体效用函数为 个纳税人,政府投资净收益由纳税人平均分享。一般个体均是风险规避的,并设个体效用函数为 ,它是个人可支配收入的连续单调递增且可微的凹函数,且假设集体中个体效用无差异。令 ,它是个人可支配收入的连续单调递增且可微的凹函数,且假设集体中个体效用无差异。令 表示没有政府投资净收益时的个体可支配收入,它是随机变量。用 表示没有政府投资净收益时的个体可支配收入,它是随机变量。用 表示政府投资的净收益和,它也是随机变量,并将其分解为两部分即确定性净收益部分 表示政府投资的净收益和,它也是随机变量,并将其分解为两部分即确定性净收益部分 和随机性净收益部分 和随机性净收益部分 (随机变量),且 (随机变量),且 , , 与 与 相互独立。用 相互独立。用 表示个体获得的政府投资净收益份额。 表示个体获得的政府投资净收益份额。
政府通过投资项目可以给个体增加可支配收入,同时投资也会带来一定的成本,这里的成本指内部成本和外部成本的总成本。此时可以分两种情况进行讨论。
第一种情况:若总成本承担者即分享政府投资净收益的集体中的个体,此时可用投资净收益表示已经涵盖了所有成本的净收益,则个体预期效用为 。假设集体中个体总数为 。假设集体中个体总数为 ,且个体在政府投资中所起的作用相同,等额分享投资的净收益,个体预期效用可表示为 ,且个体在政府投资中所起的作用相同,等额分享投资的净收益,个体预期效用可表示为 。因个体均为风险规避者,令 。因个体均为风险规避者,令 表示个体承担风险的确定性等价成本,它使得 表示个体承担风险的确定性等价成本,它使得 。在政府投资中有 。在政府投资中有 ,即当政府投资中的个体总数较大甚至趋于无穷大时,个体承担的风险等价性成本几乎为零,风险被广泛分散均衡化了。若考虑整体承担的风险等价性成本 ,即当政府投资中的个体总数较大甚至趋于无穷大时,个体承担的风险等价性成本几乎为零,风险被广泛分散均衡化了。若考虑整体承担的风险等价性成本 ,则 ,则
 (4) (4)
 (5) (5)
上式等价于
 (6) (6)
由(6)式除以(4)式可得 ,于是有 ,于是有 。这说明集体承担的风险等价性总成本随着 。这说明集体承担的风险等价性总成本随着 趋近于无穷大,它也趋近于零。若政府投资净收益分享的个体人数越多,集体的风险等价性总成本以及个体风险等价性成本都近乎为零。 趋近于无穷大,它也趋近于零。若政府投资净收益分享的个体人数越多,集体的风险等价性总成本以及个体风险等价性成本都近乎为零。
第二种情况:若政府投资产生的负外部成本不是由其投资受益集体中公众个体所承担的,而由另一 个个体所构成的集体所负担。假设 个个体所构成的集体所负担。假设 个体所承担的总成本为 个体所承担的总成本为 ,且满足 ,且满足 , , 。总成本 。总成本 是随机变量,可将其分解为确定性成本 是随机变量,可将其分解为确定性成本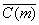 和随机性成本部分 和随机性成本部分 ,且 ,且 ,同时 ,同时 与 与 相互独立。受损害个体的效用函数仍为 相互独立。受损害个体的效用函数仍为 。该情况下只有受损害个体得到补偿,政府投资才能得以进行。令 。该情况下只有受损害个体得到补偿,政府投资才能得以进行。令 表示对受损害集体的补偿总额,并且假设 表示对受损害集体的补偿总额,并且假设 个体所得赔偿是均等的。于是可建立如下问题: 个体所得赔偿是均等的。于是可建立如下问题:
2/3 首页 上一页 1 2 3 下一页 尾页 |


