具体处理可采用指标转置的方法,即大小值和求补法,用下式计算得出处理后的指标值。设 指标值为 指标值为

式中: :处理后的指标值; :处理后的指标值; :指标最大值 :指标最大值
 :指标最小值; :指标最小值; :指标原始值 :指标原始值
第三步,确定指标权重。权重的确定方法常用层次分析法,专家评定法,两两对比法等。资源型城市可持续发展系统评价属于多目标决策问题,各指标的权重应能够反映出其对城市可持续发展的重要程度,因此我们采用层次分析法确定各层次指标的权重。
A.构造判断矩阵。由专家组成员分别对从属于上一层每个因素的同一层次各因素进行两两比较,判断各层中诸因素的相对重要性,构造各层次判断矩阵
 , , 表示对于 表示对于 而言, 而言, 对 对 的相对重要程度。 的相对重要程度。
一般 按“1~9”规则取值。见表2 按“1~9”规则取值。见表2
表21~9尺度表
|
尺度
|
含义
|
|
1
|
 与 与 的影响相同 的影响相同
|
|
3
|
 比 比 的影响稍强 的影响稍强
|
|
5
|
 比 比 的影响强 的影响强
|
|
7
|
 比 比 的影响明显的强 的影响明显的强
|
|
9
|
 比 比 的影响绝对的强 的影响绝对的强
|
|
2,4,6,8
|
 与 与 的影响之比在上述两个相邻等级之间 的影响之比在上述两个相邻等级之间
|
B.计算指标权重值。
(1)计算判断矩阵每一行元素的乘积 ; ; ( ( =1,2,…,m) =1,2,…,m)
(2)计算 的 的 次方根 次方根 : :
(3)权重计算。对向量 归一化,即可得到其权重值: 归一化,即可得到其权重值:
(4)一致性检验。判断矩阵的偏差一致性指标 : :
式中 为判断矩阵的最大特征根。 为判断矩阵的最大特征根。
(5)随机一致性比率 : :
式中 —平均随机一致性指标,可查表得出(见表3)。 —平均随机一致性指标,可查表得出(见表3)。
当 时,认为判断矩阵具有满意的一致性。 时,认为判断矩阵具有满意的一致性。
表3随机一致性指标RI的数值
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
RI
|
0
|
0
|
0.58
|
0.90
|
1.12
|
1.24
|
1.32
|
1.41
|
1.45
|
1.49
|
1.51
|
通过一系列计算和一致性检验,确定出可持续发展水平指标体系各层次的指标权重。记准则层指标 相对于目标层 相对于目标层 的权重为 的权重为 ( ( =1,2,3,4),指标层指标 =1,2,3,4),指标层指标 相对于 相对于 的权重为 的权重为 ( ( =1,2,3,4; =1,2,3,4; =1,2,…),则指标层指标 =1,2,…),则指标层指标 相对于目标层 相对于目标层 的复合权重为: 的复合权重为:
第四步,分层模糊综合评价。
可持续发展水平是相对于标准值而言的一个相对概念。而模糊数学方法的基本思想是应用模糊关系合成的原理,根据被评价对象本身存在的性态或隶属上的亦彼亦此性,从数量上对其所属成分给以刻画和描述。运用模糊数学的概念和方法建立可持续发展水平评价模型比传统的评价方法能够更符合实际的描述现状水平。根据指标体系,构建评价模型,具体思路如下:
(1)建立相关的模糊集
1)因素集
分层建立影响评价对象的各个因素组成的因素集,资源型城市可持续发展水平这一总体评价目标由准则层四个准则指标构成,定义其评价因素集 。然后,分别以准则层四个准则指标为评价对象,建立二级评价因素集: 。然后,分别以准则层四个准则指标为评价对象,建立二级评价因素集: ,( ,( =1,2,3,4; =1,2,3,4; =1,2,…)。 =1,2,…)。
2)指标权重集
通过前面第三步可以计算得出各指标的权重。记准则层 的权重集: 的权重集: ,指标层指标 ,指标层指标 相对于B的权重集: 相对于B的权重集: 。其中, 。其中, , , 都为行向量,( 都为行向量,( =1,2,3,4; =1,2,3,4; =1,2,…)。 =1,2,…)。
3)评价集
建立由 个评价结果组成的评价语集: 个评价结果组成的评价语集: ,本文取 ,本文取 =5,即将可持续发展水平分为5个等级。其中 =5,即将可持续发展水平分为5个等级。其中 代表可持续发展水平的各级评语。 代表可持续发展水平的各级评语。
(2)确定模糊评价矩阵
记因素 评价为V上的模糊子集: 评价为V上的模糊子集: ,其中 ,其中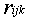 表示第 表示第 个准则下第 个准则下第 个指标隶属于第 个指标隶属于第 级评语的程度,即 级评语的程度,即 对第 对第 级评语的隶属度。从而构建出准则层第 级评语的隶属度。从而构建出准则层第 个因素的评价矩阵,即由 个因素的评价矩阵,即由 组成的隶属度矩阵。 组成的隶属度矩阵。

(3)计算隶属度
由于本文指标体系所选指标均为可量化指标,对于 的计算可通过构建隶属函数的方法确定。本文在对原始指标进行处理时,已经将所有负向指标转化为正向。 的计算可通过构建隶属函数的方法确定。本文在对原始指标进行处理时,已经将所有负向指标转化为正向。
因此,选用升半梯形分布建立一元线性隶属函数。
首先,选定各级评语的评价标准值,记为 ( ( =1,2,…,5), =1,2,…,5), 表示 表示 隶属于第 隶属于第 级评语的原始参照标准值,对负向指标的 级评语的原始参照标准值,对负向指标的 进行正向处理得到 进行正向处理得到 。评价标准值的的选取一般是依据国家或该地区对这一指标标准值的界定。 。评价标准值的的选取一般是依据国家或该地区对这一指标标准值的界定。
已知 为 为 处理后的指标值,对 处理后的指标值,对 隶属于第 隶属于第 级评语的函数关系式为: 级评语的函数关系式为:

……

……

(4)建立模糊数学模型进行综合评价
资源型城市可持续发展水平分层模糊评价共分为两层,第一层为指标层 对准则层 对准则层 的综合评价,即通过指标层各项指标权重组成的权重向量和隶属度矩阵计算评价矩阵 的综合评价,即通过指标层各项指标权重组成的权重向量和隶属度矩阵计算评价矩阵 。 。 2/3 首页 上一页 1 2 3 下一页 尾页 |


