  分别表示科研人员与大学所投入的资金, 分别表示科研人员与大学所投入的资金,  分别表示科研人员与大学所得到的分配比例,则 分别表示科研人员与大学所得到的分配比例,则 
2模型构建
科研人员的努力水平决定了大学许可技术的成功效率,大学通常为了鼓励科研人员积极参与技术转移活动,如技术的二次开发等,即使科研人员没有进行现金的投入,大学也会给予科研人员一定的提成比例 。科研人员在参与技术转移过程时会产生一个努力成本 。科研人员在参与技术转移过程时会产生一个努力成本 ,它是关于a的严格递增凸函数,当这个成本较高时, ,它是关于a的严格递增凸函数,当这个成本较高时, 通常达不到预期的激励效果,这时大学所设计的分配合同将要求科研人员注入资金来分担风险。但资金投入的同时还会产生一个投资成本 通常达不到预期的激励效果,这时大学所设计的分配合同将要求科研人员注入资金来分担风险。但资金投入的同时还会产生一个投资成本 和 和 ,其效用函数表示为: ,其效用函数表示为:

其中r为银行利率, 表示科研人员筹集资金的困难程度,大学作为一个组织其资金状况一般会好于个人,因此我们假设 表示科研人员筹集资金的困难程度,大学作为一个组织其资金状况一般会好于个人,因此我们假设 。大学科研人员的保留效用为 。大学科研人员的保留效用为 。大学科研人员通过大学技术许可所获得的收益高于其保留效用时,才愿意参与大学技术许可活动,因此必须满足参与约束: 。大学科研人员通过大学技术许可所获得的收益高于其保留效用时,才愿意参与大学技术许可活动,因此必须满足参与约束:

大学的期望效用为: ,其中 ,其中 表示大学利益分配比例, 表示大学利益分配比例, 表示大学的资金投入成本。 表示大学的资金投入成本。
大学要想使科研人员努力工作,必须保证其在高努力工作水平的收益大于低努力水平的收益,即大学设计的技术许可收益分配合同应该满足科研人员的激励相容约束:

科研人员高努力与低努力的投入成本差为: ,在这两种情况下大学技术二次开发成功的概率差为 ,在这两种情况下大学技术二次开发成功的概率差为 ,因此,激励相容约束也可以写成如下形式: ,因此,激励相容约束也可以写成如下形式:

根据委托代理理论,大学技术许可收益的分配合同应该满足:

将 , , 代入上式,得到如下委托代理合同: 代入上式,得到如下委托代理合同:
 (1) (1)
s.t. (2) (2)
 (3) (3)
 (4) (4)
 (5) (5)
设 , , , , , , 分别为式(2)、(3)、(4)、(5)的库恩-塔克乘子。其中(2)、(3)分别为科研人员的激励相容约束和参与约束,(4)、(5)为可行性约束。 分别为式(2)、(3)、(4)、(5)的库恩-塔克乘子。其中(2)、(3)分别为科研人员的激励相容约束和参与约束,(4)、(5)为可行性约束。
3模型分析
大学技术二次开发过程的复杂性和专业性决定了大学(委托人)与科研人员(代理人)之间信息来源与获取的非对称。大学难以充分、准确地观察与测量科研人员的参与程度,这为科研人员的“道德风险”创造了机会。因此,大学设计相应的激励合同来诱使科研人员付出对大学最有利的努力水平。
3.1对称信息下的大学技术许可的收益分配
对称信息下,大学技术转移过程有关信息是公开的,a是可观测变量,大学可以根据观测到的a来分配科研人员的股权比例,此时科研人员的激励相容约束条件(2)式是多余的,利用库恩-塔克定理求最大化问题(2)
 (6) (6)
 (7) (7)
所以 , , ,从而 ,从而 , ,
3.2道德风险下的大学技术许可的收益分配
由参与约束得 ,由激励相容约束条件得 ,由激励相容约束条件得 , ,
当 时,即大学科研人员为提高技术二次开发成功概率的而增加的投入相对较少时,分配比例只需满足科研人员的参与约束条件,不存在道德风险,此时的分配情况同命题1。 时,即大学科研人员为提高技术二次开发成功概率的而增加的投入相对较少时,分配比例只需满足科研人员的参与约束条件,不存在道德风险,此时的分配情况同命题1。
当 时,如果给予科研人员的分配比例过低(不满足激励相容条件),就会发生大学科研人员的道德风险,大学科研人员不会自觉努力工作。此时大学要考虑科研人员的激励相容约束,所以 时,如果给予科研人员的分配比例过低(不满足激励相容条件),就会发生大学科研人员的道德风险,大学科研人员不会自觉努力工作。此时大学要考虑科研人员的激励相容约束,所以 。根据库恩-塔克定理求最大化问题(2)得 。根据库恩-塔克定理求最大化问题(2)得 。我们接下来考虑科研人员的现金投入情况。 。我们接下来考虑科研人员的现金投入情况。
(Ⅰ)当q=0(即F)
由(7)式得 ,所以 ,所以 ,该合同只有满足式(4)和式(5)时才成立,所以 ,该合同只有满足式(4)和式(5)时才成立,所以 ,即 ,即 时, 时,
 , ,
上述结果我们可以看出,科研人员得到的分配比例与 成正比,即 成正比,即 越大,科研人员的分配比例越大。由于在(Ⅰ)中 越大,科研人员的分配比例越大。由于在(Ⅰ)中 大于 大于 。说明在非对称信息下,大学科研人员得到了更多的分配比例,因为非对称信息下,大学科研人员的努力水平无法准确观测,存在大学科研人员道德风险问题。大学为了诱使科研人员达到自己的目标,而采取激励措施,同时,要求科研人员投入资金 。说明在非对称信息下,大学科研人员得到了更多的分配比例,因为非对称信息下,大学科研人员的努力水平无法准确观测,存在大学科研人员道德风险问题。大学为了诱使科研人员达到自己的目标,而采取激励措施,同时,要求科研人员投入资金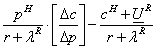 。由此,我们有 。由此,我们有
(Ⅱ)当 即 即
该合同只有在满足(3)式时才成立,即 ,故 ,故
 , ,
上述结果显示(Ⅱ)中 的值大于(Ⅰ)的值,因此在(Ⅱ)中,如果大学想要提高技术转移的成功概率,则需要科研人员更加“勤奋”,大学科研人员的努力成本增加,产生更加严重的道德风险问题。所以大学分配给科研人员更多的比例并要求其投入全部资金来诱使他们努力工作。另外,大学所获得的比例为 的值大于(Ⅰ)的值,因此在(Ⅱ)中,如果大学想要提高技术转移的成功概率,则需要科研人员更加“勤奋”,大学科研人员的努力成本增加,产生更加严重的道德风险问题。所以大学分配给科研人员更多的比例并要求其投入全部资金来诱使他们努力工作。另外,大学所获得的比例为 ,随着科研人员道德风险的增加而减少,当道德风险增加到一定程度时,即 ,随着科研人员道德风险的增加而减少,当道德风险增加到一定程度时,即 时,大学将不会进行技术许可。 时,大学将不会进行技术许可。 2/3 首页 上一页 1 2 3 下一页 尾页 |


