这样可得当 = =  时,期望效用函数 时,期望效用函数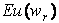 也取最大值。 也取最大值。
(2) 风险中性供应链零售商的收益
当供应链中的零售商时风险中性时,即风险规避度 (w) =0 ,将此带入④ 得到供应链中的零售商为风险中性时候的确定收益为 (w) =0 ,将此带入④ 得到供应链中的零售商为风险中性时候的确定收益为 =βka - =βka -
2. 供应链中供应商的收益
设 为供应商的随机收入,则供应链供应商收益为供应商业绩与零售商报酬之差额,即 为供应商的随机收入,则供应链供应商收益为供应商业绩与零售商报酬之差额,即
 = =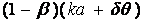 ⑥ ⑥
下面分别给出委托人风险中性和风险规避情况下的收益。
(1)风险规避供应商的收益
当供应链中的供应商是风险规避时,也采用Arrow-Pratt 绝对风险规避度 来描述其风险规避程度: 来描述其风险规避程度:  = - = - / / >0 >0
由式 ⑥ 及假设3,得到 ~ N ((1-β)ka ,(1-β) )。也假定供应链中的供应商的效用函数具有不变绝对风险规避特征,则供应商的效用函数为u( ~ N ((1-β)ka ,(1-β) )。也假定供应链中的供应商的效用函数具有不变绝对风险规避特征,则供应商的效用函数为u( )=- )=- 。与上节风险规避零售商的收益计算过程相类似,供应链中供应商的效用函数期望值为 。与上节风险规避零售商的收益计算过程相类似,供应链中供应商的效用函数期望值为
 = = ⑦ ⑦
根据确定性等值的定义: Eu( )=u( )=u( ), ),
可得:  ⑧ ⑧
根据式⑦ , 有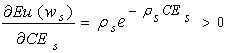 , 则最大化期望效用函数 , 则最大化期望效用函数 等价于最大化确定性等价收入式⑧ 。 等价于最大化确定性等价收入式⑧ 。
(2) 风险中性供应商的收益
当供应链中的供应商是风险中性,即风险规避度 =0时,将此式带入⑧,得到供应链中的供应商为风险中性时的确定收益 =0时,将此式带入⑧,得到供应链中的供应商为风险中性时的确定收益  = = 。 。
(五) 非对称信息下的利益分配比例的确定
在供应链的供应商对零售商的努力程度具有非对称的信息时,供应商所面临的问题是在考虑零售商的利益的情况下,设计适当的契约——确定契约中的收入提成比例 和固定值 和固定值 ,以促使零售商努力工作,从而使供应商自己利益最大化。 ,以促使零售商努力工作,从而使供应商自己利益最大化。
由于供应链的零售商是具有独立利益的主体,在供应链中的供应商给出契约之后,零售商将会考虑自己的利益,确定最优的努力水平以最大化自己的收益。同时,零售商参与供应链中产品的最低条件是他所得到的收益不能低于其保留收益,否则零售商就不会参与到供应链里来。为此可以构建模型:
max   ⑨ ⑨
s.t. max = = ⑩ ⑩
 = =   W1 [③] 11 W1 [③] 11
在这个模型中包含了参与人的4中不同风险偏好组合情况:
①当 , , 时,供应链中的供应商和零售商均为风险中性 时,供应链中的供应商和零售商均为风险中性
 ②当 ②当 , , >0 时,零售商为风险中性的,供应商为风险规避的 >0 时,零售商为风险中性的,供应商为风险规避的
③当 , , =0时, 零售商为风险规避的,供应商是风险中性的 =0时, 零售商为风险规避的,供应商是风险中性的
④当 , , 时,供应链中的供应商和零售商都是风险规避 时,供应链中的供应商和零售商都是风险规避
将式⑤取代⑩ ,即可得到与之等价的模型。在Kuhn-Tucker 最优性条件下,此模型中的不等式11的等号成立[5]。将⑤和11的等式代入⑨,有 12 12
对式12分别进行一阶、二阶微分供应商,由于 ,令 ,令 ,就可以得到使供应商收益最大时的零售商最优提成 ,就可以得到使供应商收益最大时的零售商最优提成  13 13
最佳的固定支付:
 14 14
将13代入12式,可得供应链的供应商的收益为 15 15
这样就可以得到一个最优的收益分配合约。在这个合约下,可以使供应链的供应商和零售商的期望效用最大。
三.结果分析
通过构建的供应链收益分配模型可以得出,在供应商和零售商信息不对称的条件下,供应商也能够利用合理的收入契约激励零售商努力工作,使其确定性等价收入最大,令零售商对其收益满意。在此同时可以使自身的收益也达到最大。
由以上分配模型可以看出,供应链中的企业越是风险规避的,供应商的整体收益也是越少的,整个供应链的收益也是越少的。为此作为供应链的核心企业的供应商不应该对风险太保守。供应商在选择零售商时应该充分考虑它的风险偏好问题。因为风险越是规避的零售商,供应链获得收益就会越少。
供应链成员企业的风险偏好态度对无论是对供应链的整体收益还是对供应商、零售商的收益都有重要影响。
四、结论
供应链成员企业之间很多情况下都存在着信息不对称的情况,如何在这种条件下,合理的进行供应链的利益的分配是保证供应链健康发展的重要基础条件。为此本文利用委托-代理理论的思想构建了在信息不对称条件下,考虑到供应链成员企业不同风险偏好的供应链利益分配模型。揭示了当供应链存在信息不对称现象以及成员企业有不同的风险偏好的时候,供应链的利益应该如何分配才能使供应链的企业收益最大化。
参考文献
[1]孙永军,潘晓弘,程耀.基于委托-代理机制的供应链合作关系模型[J].高技术通讯.2002,(10):54-57.
[2]李志方,刘威,程国平.基于不确定需求的供应链利润分配策略研究[J].工业技术经济.2008,27(8):91-93.
[3]张维迎.博弈论与信息经济学[M].上海:上海人民出版社, 1996:256-262.
[4]Kim S K, Wang S S. Linear contracts and the doublemoral hazard [J]. Journal of Economic Theory, 1998, 82 (3):342-378.
[5]田厚平,刘长贤,吴萍.非对称信息下参与人不同风险偏好组合的委托代理问题[J]. 管理工程学报. 2007,21(3):24-28.
2/2 首页 上一页 1 2 |


