用好速度分解模型,防止解题陷阱例析
论文关键词:速度分解模型,解题陷阱,例析
当船B向右拉小车动时(图2),同样可得V1=V车=V船Cosθ,V2=V船Sinθ,船的实际速度为合速度,沿绳方向和垂直与绳方向为分速度方向很直观,其方法在求解涉及速度变化,隐含“陷阱”一类题目,显得十分实用简明,下面看常见几例。
二、例1,如图3,竖直平面内固定一半径为R的半圆形圆柱截面,用轻质不可伸长且足够长的细线连接AB两球,质量分别为M,m现将球A从圆柱边缘处静止释放,已知A球始终不离开球面且不计一切摩擦,求A球滑止最低点时,两球速度大小。
错解:如图4,MgR-mg 共2 共2
分析;认为A在最低点两球速度相等是陷阱。

正解:A到最低点,两球速度不等,A球运动有两种效果,沿绳方向使绳伸长,垂直于绳方向使绳摆动,且VA在绳方向上的投影等于VB。
MgR-mg A2+ A2+ B2 B2
VAsin45°=VB 联立得:VA = 2 VB = VB =
例2.如图5,A、B质量mA=mB=3.75kg,C的质量mC=1kg,A、B放在处于同一高度的光滑水平台面上,AB之间用一足够长轻绳(无弹性)连接,DE分别是两个大小不计的光滑定滑轮,DE间距1.2m,将重物C用一光滑轻钩挂在绳子DE中点,开始时用手托住C,使绳子水平拉直,然后从静止释放,当C下落h=0.8m时,求A、B、C速度VA、VB、V C 大小。
  图5 图5
错解1:A、B、C速度相等,由mcgh= (mA+ mB + mC)V共2 (mA+ mB + mC)V共2
V共=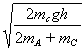 =1.37m/s =1.37m/s
分析:认为A、B、C速度相等是陷阱,只有当DE宽度小到忽略不计时上式成立。
错解2:由图6得A、B、C位移关系可知VA=VB,
VC = (VA Cosθ+VBCosθ) (VA Cosθ+VBCosθ)
=VACosθ
= ………………………………………………① ………………………………………………①
再考虑能量守恒有:
= + + + + ………………② ………………②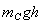
联立解得VC=1.12m/s,VA=VB=1.40m/s.
此解法随考虑了速度分解,但分解方法错误。
正解:如图7,由位移关系知C下落时VA=VB<VC , 位移关系为, - - <h, VC可分解为沿绳方向的速度V1=VA,使绳绕D摆动速度分量V2, <h, VC可分解为沿绳方向的速度V1=VA,使绳绕D摆动速度分量V2,
即V1 = VA = VCcosθ=  …………(1) …………(1)
由机械能守恒:mcgh = mCVC2+2× mCVC2+2× mAVA2…………(2) mAVA2…………(2)
联立①②代入数据得:VC =1.35m/s. VA =1.08m/s.
例3.在匀强电场中有一长 的轻质绝缘不可伸长的细线,上端悬于O点,另一端系一质量为m的带电小球,电场方向水平向右,小球能静止在A点,保持平衡此时,细线与竖直方向夹角30°,现将小球拉到B点,使细线水平拉直,由静止释放小球,试求小球运动到最低点D时的速度大小及对细线的拉力大小。 的轻质绝缘不可伸长的细线,上端悬于O点,另一端系一质量为m的带电小球,电场方向水平向右,小球能静止在A点,保持平衡此时,细线与竖直方向夹角30°,现将小球拉到B点,使细线水平拉直,由静止释放小球,试求小球运动到最低点D时的速度大小及对细线的拉力大小。
错解:如图8,小球在A点平衡,qE = mgtan30°= mg………… (1) mg………… (1)
从B到D,由动能定理:mg +qE +qE = = mvD2…………(2) mvD2…………(2)
T-mg =m …………………………………………………(3) …………………………………………………(3)
联立①②③VD =
T =(3+ )mg )mg
图8
分析:认为小球一直做圆弧运动是陷阱。
正解:小球从B到D除受重力外,还受电场力作用,先做匀加速直线运动到C后圆弧运动到D,当qE= mg时,∠B=60°。 mg时,∠B=60°。
从B到C用动能定理:mg Lsin60°+qE Lsin60°+qE L= L= mVC2…………① mVC2…………①
VC在C点欲使得绳伸长产生沿绳的分量Vn ,使绳绕O摆动的切向分量Vτ,Vn瞬间变为零,对应动能转化为内能,小球以Vτ开始做圆弧运动,由几何关系:Vτ=VC·cos30°…………………………………②
从C到D,由动能定理,
qE L +mg L +mg (1-cos30°)= (1-cos30°)= mVD2- mVD2- mVτ2……………③ mVτ2……………③
T-mg =m ……………………………………………………④ ……………………………………………………④
由①、②、③、④得:VD =
线张力T = mg(3+ ) )
例4.长L=2m不可伸长轻绳一段固定于O点,另一端系质量为m=100g小球,将小球从O点的正下方h=0.4m处水平向右抛出,经一段时间绳被拉直,此时绳与竖直方向53°,此后小球以O点为悬点在竖直面内转动。试求小球最低点时绳所受拉力。
错解:如图9, mVB2+mgL(1-cos53) = mVB2+mgL(1-cos53) =  mVD2求速度等。 mVD2求速度等。

 图9 图9
正解:Lcos53°-h = gt2…………① gt2…………①
Lsin53°= Vx t…………………………②
由①②得,t = 0.4s,Vx = 4m/s
Vy = gt = 4m/s
所以 VB = 4 m/s VB与竖直方向45° m/s VB与竖直方向45°
V1 = VB Cos(45°+37°) = 0.78m/s
设小球在最低点速度VD,由 mV12+mg(1-cos53°)= mV12+mg(1-cos53°)=  mVD2……③ mVD2……③
T-mg = m ……④ ……④
拉力T = 1.83N
以上四例,形异而质同,错解来自于忽视了整个运动过程中各时刻状态的分析,缺少运动各时刻速度的正确分解。只要牢记:“湖面船离岸、靠岸”情景下,船速度分解模型,就能回避“陷阱”,得出正确结果。对绳连体出现绳子突然绷紧,速度瞬间变化,系统部分机械能及其他能转化为内能的一类习题,尤为方便可靠。
|


