论文导读::反比例函数与面积法,初中数学论文。
论文关键词:反比例函数,面积法
面积法应用广泛,方法巧妙,在与反比例函数相关的题中,若能充分利用,并借助基本图形,将大大提高解题速度.
基本图例1:如图1,易证S△ABO =S△ACO = xy= xy= ∣k∣初中数学论文初中数学论文,S矩形ABCO=∣k∣ ∣k∣初中数学论文初中数学论文,S矩形ABCO=∣k∣
  基本图例2:如图2,如果AD∥BC,按同底等高的三角形面积相等,可得到S△ABC =S△DBC,反之,如果S△ABC =S△DBC,得到AE=DF,则有矩形AEFD,所以也可得到AD∥BC, 基本图例2:如图2,如果AD∥BC,按同底等高的三角形面积相等,可得到S△ABC =S△DBC,反之,如果S△ABC =S△DBC,得到AE=DF,则有矩形AEFD,所以也可得到AD∥BC,

例1 如图,在直角坐标平面内,函数 ( x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1.过点A作AC⊥x轴于C,过点B作BD⊥y轴于D,连接AD、BC、DC.(1)证明:AB∥CD ( x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1.过点A作AC⊥x轴于C,过点B作BD⊥y轴于D,连接AD、BC、DC.(1)证明:AB∥CD
(2)若△ABD的面积是4初中数学论文初中数学论文,求B点坐标,
解析:(1)分别作AP⊥y轴于P,BQ⊥x轴于Q
由基本图例1可知:S矩形APOC= S矩形BQOD=∣m∣
于是有S矩形APDN =S矩形BQCN S△ADN =S△BCN S△ADN =S△BCN
S△ADC =S△BCD,再根据基本图例2,于是可证出AB∥CD
(2)∵ S△ABD =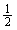 BD?AN= BD?AN=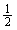 a(4-b) a(4-b)
∴ 4=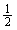 a(4-b)= 2a- a(4-b)= 2a-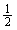 ab 由基本图例1可知 ab 由基本图例1可知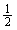 ab= ab=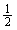 ×1×4=2 ×1×4=2
解得a=3,b= 所以B点坐标是(3, 所以B点坐标是(3, ) )
例2 (09山东威海)一次函数 的图象分别与x轴、y轴交于点M、N,与反比例函数 的图象分别与x轴、y轴交于点M、N,与反比例函数 的图象相交于点A、B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C、E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD. 的图象相交于点A、B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C、E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.
(1)若点A、B在反比例函数 的图象的同一分支上,如图1初中数学论文初中数学论文,试证明: 的图象的同一分支上,如图1初中数学论文初中数学论文,试证明:
①S四边形AEDK =S四边形CFBK;②AN=BM.
(2)若点A,B分别在反比例函数 的图象的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论. 的图象的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论.
解析:(1)①由基本图例1可知:S矩形AEOC= S矩形BDOF=∣k∣
∴ S矩形AEOC-S矩形KDOC=S矩形BDOF-S矩形KDOC
∴ S四边形AEDK =S四边形CFBK
②按例1思路易证AB∥CD ,而且AC ∥DN, BD∥CM
∴ 有平行四边形ACDN和平行四边形BDCM,于AN=CD,BM=CD
所以AN=BM
(2)连接AD、BC,由基本图例1可知:S矩形BDOF= S矩形ACOE=∣k∣
∴ S矩形AEOC+S矩形KDOC = S矩形BDOF+S矩形KDOC 即S四边形AEDK =S四边形CFBK
∴ S△ADK =S△BCK ∴ S△ADK-S△CDK=S△BCK-S△CDK 即S△ACD =S△BCD
再按基本图例2思路易证AB∥CD
于是有平行四边形ACDN和平行四边形BDCM,于AN=CD,BM=CD
所以AN与BM仍然相等
|


