所以上面问题的解 的有效性还需要经过下面模型的检验才可以。
第二阶段：
检验的有效性或者寻找新的有效解
 
如果=，那说明已经是问题的最优解。如果两个解不相等，那不是有效
但是总是有效解。所以在任何情况下，两阶段法总是可以在第2阶段保证第原问
题的有效解.
（4）模型的算例分析
假设下面是专家给出的8种证券的模糊收益率运用前面所建立的模型，结合算法进行实证分析。
专家给出的股票模糊收益率
股票
1
（0.009，0.0163，0.018）
2
（0.236，0.33，0.414）
3
（0.207，0.253，0.277）
4
（0.0807，0.0918，0.1028）
股票
5
（0.1448，0.1646，0.184）
6
（0.022，0.028，0.034）
7
（0.226，0.343，0.424）
8
（0.015，0.021，0.026）
股票的预期收益率和风险损失率
股票
收益率
风险损失率
1
0.0144
0.0008
2
0.3267
0.0148
3
0.2457
0.0060
4
0.0918
0.0018
股票
收益率
风险损失率
5
0.1645
0.0033
6
0.028
0.001
7
0.331
0.0167
8
0.0207
0.0009
将数据代入上面研究的模型 中分析得：
第一步：求得
得相应的隶属函数为
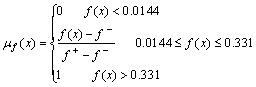
解相对应的线性问题：
 
得 , ，收益率为0.2347，风险为0.0056.
第二步：检验以上求的解是不是原问题的有效解。
得 ,  收益率为0.2347，风险为0.0056计算结果表明，8种证券组合投资比例为：对于证券3，投资比例为0.8647；对于证券5，投资比例为0.1353；其余股票投资比例为0.
4、小结
本文利用了模糊收益率下的风险损失率定义，建立了一个多目标的投资组合模型，其中预期收益率最大化和投资组合风险损失率最小，由于多目标规划问题的绝对最优解往往是不存在的，因而采用两阶段算法找出模型的有效解，并给出算例进行说明，从算例的结果看出，关于风险损失率的定义能在投资组合模型中得到较好的应用。
参考文献
[1]陈国华、廖小莲.多目标投资组合模型的模糊两阶段解法[J].吉首大学学报，2006，第27卷：18-21.
[2]林军，卢谦.模糊预期收益率下风险损失率的左偏差度量[J].模糊系统与数学，2002，16（3）：87-93
[3]许若宁，李楚霖.衡量模糊标志值[J].模糊系统与数学，2001，第15卷第1期：62-67.
2/2 首页 上一页 1 2 |
