|
  
图2顶端边界点 处各物理量的时程曲线 处各物理量的时程曲线
Fig2. Time-history curves of physical quantitiesat the vertex on the top on the top
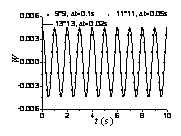  
图3顶端中点 处各物理量的时程曲线 处各物理量的时程曲线
Fig3. Time-history curves of physical quantitiesat the midpoint on the top on the top
图4给出了在 时刻,布点为 时刻,布点为 ,时间步长为 ,时间步长为 时,四种不同材料地基,即孔隙热弹性2维地基(TEVF)、孔隙弹性2维地基(EVF)、热弹性2维地基(TEF)、弹性2维地基(EF),顶端沉降、孔隙百分比和温度随X的变化曲线。可以看到,孔隙的存在使沉降和温度有所增加,而温度的影响则使沉降减小和孔隙体积百分比增加,这是因为能量部分转换成热能,引起耗散的结果。 时,四种不同材料地基,即孔隙热弹性2维地基(TEVF)、孔隙弹性2维地基(EVF)、热弹性2维地基(TEF)、弹性2维地基(EF),顶端沉降、孔隙百分比和温度随X的变化曲线。可以看到,孔隙的存在使沉降和温度有所增加,而温度的影响则使沉降减小和孔隙体积百分比增加,这是因为能量部分转换成热能,引起耗散的结果。
  
图4  时刻,各物理量随X的变化曲线 时刻,各物理量随X的变化曲线
Fig.4 Variation of physical quantities with X at
计算中,还画出了经过10个周期后,在不同时刻 ,沉降、孔隙百分比和温度的等势图,限于篇幅不再列出。从这些图中看到,沉降、孔隙百分比和温度随时间的变化从对称分布变为反对称分布。表1给出了时间步长 ,沉降、孔隙百分比和温度的等势图,限于篇幅不再列出。从这些图中看到,沉降、孔隙百分比和温度随时间的变化从对称分布变为反对称分布。表1给出了时间步长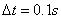 ,在 ,在 时刻,不同布点情况下,顶端中点 时刻,不同布点情况下,顶端中点 处沉降、孔隙百分比和温度值的比较。可以看出,结果是收敛的。 处沉降、孔隙百分比和温度值的比较。可以看出,结果是收敛的。
表1 布点对顶端中点 处各物理量的影响( 处各物理量的影响( ) )
Table 1Effect of the node distribution on physical quantities at the midpoint on the top ( on the top ( ) )
|
|

|

|

|

|

|
|

|
4.3630E-3
|
4.3690E-3
|
4.3680E-3
|
4.3664E-3
|
4.3651E-3
|
|

|
-6.4614E-3
|
-6.6451E-3
|
-6.6801E-3
|
-6.6829E-3
|
-6.6806E-3
|
|

|
-5.7120E-3
|
-6.0142E-3
|
-6.1534E-3
|
-6.2299E-3
|
-6.2778E-3
|
计算中,还数值地研究了各参数的影响。可以看到,不同的参数对各物理量的影响是不尽相同的,例如,孔隙体积百分比随孔隙率变化扩散系数 的增加而减小物理论文,温度随 的增加而减小物理论文,温度随 的增加而增加,沉降随 的增加而增加,沉降随 的增加而略有减小。沉降、孔隙体积百分比和温度都随位移-孔隙耦合数 的增加而略有减小。沉降、孔隙体积百分比和温度都随位移-孔隙耦合数 的增加而显著增加。孔隙体积百分比和温度随孔隙-温度耦合参数 的增加而显著增加。孔隙体积百分比和温度随孔隙-温度耦合参数 的增加而增加,而沉降增加较少。但是,孔隙体积百分比和温度随孔隙-温度耦合参数 的增加而增加,而沉降增加较少。但是,孔隙体积百分比和温度随孔隙-温度耦合参数 的增加是先增后减,沉降随 的增加是先增后减,沉降随 的增加而略有增加。还可以看到,孔隙体积百分比和温度随位移-温度耦合参数 的增加而略有增加。还可以看到,孔隙体积百分比和温度随位移-温度耦合参数 的增加而增加,但是沉降则随 的增加而增加,但是沉降则随 的增加而略有减小。 的增加而略有减小。
3.2 在周期性温度载荷作用下地基的动力学响应
假设给定周期性温度载荷为 ,利用同样的求解方法和参数进行了数值计算。计算中取 ,利用同样的求解方法和参数进行了数值计算。计算中取 ,表2给出了在时刻 ,表2给出了在时刻 时,顶端中点 时,顶端中点 处沉降、孔隙体积百分比和温度的数值结果。可以看出,随着耦合参数 处沉降、孔隙体积百分比和温度的数值结果。可以看出,随着耦合参数 的增加,孔隙体积百分比增加,温度则减小。沉降随 的增加,孔隙体积百分比增加,温度则减小。沉降随 的增加而增加,随 的增加而增加,随 的增加而减小。 的增加而减小。
表2 顶端中点 处各物理量的值( 处各物理量的值( ) )
Table 2 Values of physical quantities at the midpoint on the top ( on the top ( ) )
|
TEVHF
|

|

|

|

|
|

|
1.349E-3
|
1.229E-3
|
1.463E-3
|
1.236E-3
|
|

|
-7.181E-3
|
-2.188E-3
|
-6.251E-3
|
-2.476E-3
|
|

|
3.869E-2
|
3.924E-2
|
4.062E-2
|
3.918E-2
|
3.3 极限车载作用下地基的动力学特性
考察如图5所示深度为 的孔隙热弹性无限长的岩土场地上,每隔一定的车间距 的孔隙热弹性无限长的岩土场地上,每隔一定的车间距 ,都有一辆质量相等的车沿着相同的方向等速前行。给定车重 ,都有一辆质量相等的车沿着相同的方向等速前行。给定车重 ,车速(移动荷载行进的速度) ,车速(移动荷载行进的速度) ,轮间距 ,轮间距 。 。
 
图5极限移动车载下地基的物理模型
Fig. 5 Physical model of foundation subjected to a limitmoving vehicle load
从图5所示岩土地基物理模型中取出一个周期性区域 来进行分析,则在每个周期区域中的车辆载荷可以给定为 来进行分析,则在每个周期区域中的车辆载荷可以给定为
 (14) (14)
其中, , , , , 为取整函数。在运用DQM来进行数值模拟时,作用在第 为取整函数。在运用DQM来进行数值模拟时,作用在第 和 和 个节点上的载荷可以近似表示为(图6) 个节点上的载荷可以近似表示为(图6)
 (15) (15)
3/4 首页 上一页 1 2 3 4 下一页 尾页 |


