顶部边界 处的边界条件为 处的边界条件为
 (7a) (7a)
其中, 为周期外力和温度的无量纲量。而 为周期外力和温度的无量纲量。而 , , 为物体和空气的对流换热系数。当 为物体和空气的对流换热系数。当 时为绝热边界条件, 时为绝热边界条件, 时为等温边界条件。 时为等温边界条件。
底部边界 处的边界条件为 处的边界条件为
 (7b) (7b)
侧向周期边界 处,应该满足如下周期性条件:(1)介质的位移相等;(2) 介质的法向和切向应力相等;(3)孔隙百分比相等;(4)温度相等;(5)外法线方向孔隙百分比发展相等;(6)外法线方向温度导数相等。并有如下表达式: 处,应该满足如下周期性条件:(1)介质的位移相等;(2) 介质的法向和切向应力相等;(3)孔隙百分比相等;(4)温度相等;(5)外法线方向孔隙百分比发展相等;(6)外法线方向温度导数相等。并有如下表达式:
 (7c) (7c)
其中, 和 和 分别是边界 分别是边界 和 和 上的法向应力和切向应力, 上的法向应力和切向应力, 和 和 分别是 分别是 和 和 的单位外法线矢量。 的单位外法线矢量。
1.3 初始条件
对于未变形的孔隙热弹性介质,当 时,有初始条件 时,有初始条件
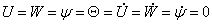 (8) (8)
这样,公式(5)-(8)构成了在移动周期性载荷作用下,孔隙热弹性地基动力响应问题的基本场方程。我们将采用微分求积法(DQM)和有限差分法(FDM)在空间域和时间域内来离散控制方程并求解,由此研究在移动周期载荷作用下孔隙热弹性地基的动力学特性。
2控制方程的离散化与求解
2.1 控制方程的DQ离散化
微分求积法(DQM)是将函数对某方向的自变量的偏导数近似表达为其各离散点(节点)上相应函数值的加权和,其加权系数取决于节点分布并与具体问题无关。因此,利用这些系数,任何微分方程都能转化为相应的代数方程。关于DQM可参考文献[13]和其他近期的相关文献[14]。根据文献[13],可得控制方程(5)在空间域内的DQ离散化形式

 (9) (9)
其中, 表示对X的m阶偏导数的权系数, 表示对X的m阶偏导数的权系数, 表示对Z的n阶偏导数的权系数。这里,采用多项式作为试函数来构造权系数,并利用Chebyshev-Lobatto多项式的零点的来布置节点的坐标[13]。 表示对Z的n阶偏导数的权系数。这里,采用多项式作为试函数来构造权系数,并利用Chebyshev-Lobatto多项式的零点的来布置节点的坐标[13]。
2.2边界条件的DQ离散化
同样根据[13],也可得到边界条件的DQ离散化方程。
顶部处边界条件的DQ离散化形式为
 (10a) (10a)
底部处边界条件的DQ离散化形式为
 (10b) (10b)
周期性边界 和 和 处周期性边界条件的DQ离散化形式为 处周期性边界条件的DQ离散化形式为
 (10c) (10c)
初始条件的DQ离散化形式为
 (10d) (10d)
方程(9)-(10),组成了周期域 内平面孔隙热弹性动力学特性分析的初边值问题的空间DQ离散化方程组。 内平面孔隙热弹性动力学特性分析的初边值问题的空间DQ离散化方程组。
2.3 时间导数的离散
能够看到,空间域内的DQ离散化控制方程(9)-(10)是关于时间的微分-代数方程组,求解一般比较困难。为了方便,将其写成矩阵形式
 (11) (11)
其中, 为未知量组成的矢量,即它是所有要求的未知量 为未知量组成的矢量,即它是所有要求的未知量 在离散点 在离散点 处的值构成的矢量发表论文。 处的值构成的矢量发表论文。 和 和 是所有未知函数对时间 是所有未知函数对时间 的导数项的系数构成的矩阵,它们是奇异的, 的导数项的系数构成的矩阵,它们是奇异的, 是由相关未知量空间离散所得代数函数组成的矢量。采用一阶和二阶向后差分格式来逼近时间导数,即 是由相关未知量空间离散所得代数函数组成的矢量。采用一阶和二阶向后差分格式来逼近时间导数,即
 (12) (12)
其中物理论文, 为当前时刻的无量纲量。利用公式(12),原系统(9)-(10)可以被转化为一组代数方程 为当前时刻的无量纲量。利用公式(12),原系统(9)-(10)可以被转化为一组代数方程
 (13) (13)
当给定初值时,利用通常的迭代方法可求得当前时刻为止的位移矢量 。计算中,取真实时间步长 。计算中,取真实时间步长 , ,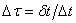 为微小的真实时间 为微小的真实时间 的无量纲量。 的无量纲量。
3 孔隙热弹性地基的动力学响应
3.1 在移动周期谐载荷作用下的动力学响应
在图1所示的物理模型中,给定移动谐载荷为 ,其中, ,其中, 是波数, 是波数, 是波长; 是波长; 是频率, 是频率, 是周期。计算中,给定参数如下[12,15]: 是周期。计算中,给定参数如下[12,15]:

对应的无量纲参数为

利用前述的离散化和求解方法,可得问题的数值解。图2和图3分别为顶端边界点 和中点 和中点 处的沉降、孔隙体积百分比和温度的时程曲线。计算中,采用三种布点方式,即 处的沉降、孔隙体积百分比和温度的时程曲线。计算中,采用三种布点方式,即 , , 和 和 ,而 ,而 分别为时间步长。由图看出,不同的时间步长和布点得到的时程曲线是一致的。说明本文方法具有良好的收敛性。 分别为时间步长。由图看出,不同的时间步长和布点得到的时程曲线是一致的。说明本文方法具有良好的收敛性。
2/4 首页 上一页 1 2 3 4 下一页 尾页 |


